Transiciones Termodinámicas y Coherencia de Fase en Superconductores de Alta Temperatura
Anisotropía
Una de las propiedades más destacables de los superconductores basados en óxidos de cobre es que tanto sus propiedades en el estado normal como las que corresponden al estado superconductor muestran una gran anisotropía. Esa anisotropía refleja aquella que se evidencia en la estructura atómica
Los datos experimentales indican que la conductividad eléctrica es mucho mayor en la dirección de los planos de Cu-O (dirección ab) que en la dirección perpendicular a ellos (dirección c). Tenemos así una resistividad ab y una c. Una forma de definir la anisotropía del material es a través del cociente de resistividades en sus direcciones principales h = c /ab. Estos valores cambian desde el que corresponde al YBa2Cu3O7 h50, considerado como moderadamente anisotrópico, hasta los que corresponden a los materiales de mayor anisotropía, como el Bi2Sr2CaCu2O8, en el cual el cociente h20.000 pone de manifiesto la anisotropía extrema que caracteriza a estos materiales. Hemos demorado el análisis de la influencia de la anisotropía, no porque su efecto sobre las propiedades que discutimos sea de carácter secundario sino por que la anisotropía esencialmente solo modifica cuantitativamente la manifestación de esas propiedades
Para las anisotropías mayores, las propiedades físicas de los superconductores se pueden interpretar suponiendo que la superconductividad tiene un carácter cercano al bidimensional. La superconductividad se nuclea solamente en los planos de Cu-O. Las funciones de onda de los pares de Cooper en planos vecinos se superponen débilmente, permitiendo la existencia de efecto túnel (efecto Josephson) de pares entre planos. Este acoplamiento establece el carácter tridimensional del superconductor, induciendo la coherencia de fase en la dirección c.
La descripción teórica de la superconductividad en los sistemas laminares débilmente acoplados fue desarrollada por Lawrence y Doniach para describir el comportamiento de superconductores laminares convencionales, preparados artificialmente. Utilizando conceptos presentados en la teoría se puede interpretar algunas de las características cuasi-bidimensionales de los SAT. Resultados experimentales, que se discuten en este artículo muestran que aun el sistema YBa2Cu3O7 presenta características sólo esperables, de acuerdo a las concepciones teóricas aceptadas, en sistemas mucho más anisotrópicos. Creemos importante discutir resultados que se esperaría obtener en sistemas altamente anisotrópicos pues, a nuestro entender, ponen de manifiesto el comportamiento experimental, aun en sistemas que se consideran moderadamente anisotrópicos.
En una imagen laminar se considera que los planos superconductores se acoplan a través de láminas aisladoras. Dos tipos de corrientes superconductoras se pueden sostener en el sistema: las que circulan en los planos y asociadas a los correspondientes gradientes de la fase del parámetro de orden y las que, por efecto túnel, atraviesan los planos de Cu- O. En este último caso la corriente no está determinada por gradientes. El efecto Josephson explica el paso de corriente a través de junturas aisladoras, introduciendo una relación constitutiva no lineal entre la corriente y la diferencia de fase entre láminas. No puede haber corrientes determinadas por trayectorias que se localizan entre planos, pues no puede haber estados de pares con vida media infinita en la zona aisladora.
FIGURA 1
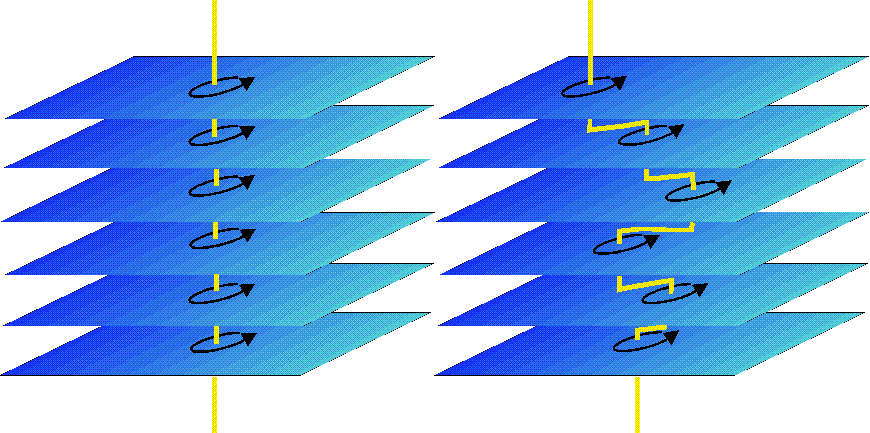
Figura 1. Esquema de la estructura de un vórtice en un SAT a temperatura nula y a temperatura finita. Las flechas representan las corrientes en los planos de CuO3
Un dibujo esquemático de cómo imaginamos un vórtice en un sistema bidimensional se muestra en la figura 2. Las corrientes se distribuyen en órbitas concéntricas sobre los planos, denominadas panqueques. Para minimizar la energía de línea del vórtice los panqueques se colocan uno encima de otro. Si las corrientes no fuesen superconductoras, esta disposición determina unívocamente la dirección del campo. Como la distancia entre planos es mucho menor que la distancia l(T) 1500 Å donde circula la corriente el resultado sería una distribución de campo indistinguible de la que corresponde a un vórtice continuo. Sin embargo, hay que tener en cuenta la relación constitutiva que gobierna la corriente superconductora. Para que no circulen corrientes en la dirección del eje c y de esa forma minimizar la energía cinética y de campo es necesario tener la fase del parámetro de orden igual entre todos los planos que constituyen la muestra laminar. Esto es, la fase cambiará en 2 en cada capa tantas veces como vórtices haya pero entre planos la diferencia de fase debe anularse.
Como los fenómenos físicos correspondientes al equilibrio termodinámico se manifiestan minimizando la energía libre y no necesariamente la interna, nos vemos obligados a analizar las excitaciones en un sistema laminar. Vimos cómo la teoría imaginaba la introducción de excitaciones de flujo magnético, en forma de toroides. Debemos pensar en formas similares que cumplan con los requerimientos de cuantificación de flujo, y que permitan introducir entropía en el sistema de panqueques. La forma más simple de introducir entropía en un sistema laminar es producir desplazamientos relativos entre panqueques en cada plano y de cada uno de ellos con relación a su vecino en el plano superior e inferior, ver fig. 2. Como al desplazarse las corrientes se introducen diferencias de fase entre planos, el desplazamiento irá acompañado de corrientes Josephson entre ellos. Como el flujo magnético debe ser conservado en forma de cuantos, las corrientes entre planos generan "vórtices Josephson" que interconectan los panqueques en los planos. Por comparación con la figura... lo que en ella eran desviaciones curvilíneas del vórtice se convierte aquí en desviaciones en forma de escalera, con dos tipos de corrientes. La energía de la excitación se compondrá de términos asociados a los panqueques y términos asociados a los tramos de vórtices Josephson.
Distinguir experimentalmente un sistema muy anisotrópico de uno laminar. es de hecho muy difícil, aunque conceptualmente son totalmente distintos. El sistema anisotrópico se describe a través de una anisotropía en los parámetros superconductores, indicando que cuesta menos energía distribuir corrientes en las direcciones ab que en c. Sin embargo un vórtice en la dirección ab tendrá corrientes superconductoras alrededor del núcleo que están contenidas en las regiones entre planos. La forma más segura de detectar un verdadero comportamiento laminar es realizar experimentos que pongan de manifiesto la existencia de junturas Josephson. Hasta ahora esto sólo se ha mostrado en los compuestos de Bi2Sr2CaCu2O8. Pese a ello, muchos resultados experimentales se pueden describir con mayor facilidad a través del modelo laminar.
Ahora que hemos discutido las características anisotrópicas de los superconductores, resulta evidente que cuanto más anisotrópico sea el superconductor más fácil será introducir excitaciones en forma de vórtices cerrados. Vemos así, la importancia que adquiere la constante C44 en la aproximación elástica del tratamiento de la interacción entre vórtices.
Propiedades de los Superconductores Convencionales
El llamado estado mixto en los superconductores tipo II ha sido objeto de intenso estudio en el pasado y en el presente. El hecho de que el estado mixto es un estado de equilibrio termodinámico fue aceptado mucho después de descubrirse el fenómeno de la superconductividad y aun después de haberse conseguido la formulación teórica que explicaba tanto su manifestación fenomenológica, a través de la teoría de Ginsburg-Landau, G-L, como su origen microscópico a través de la teoría de Bardeen, Cooper y Schrieffer, BCS.
La teoría que describe el estado mixto se debe a Abrikosov y fue dada a conocer después que Feynman describió los vórtices como excitaciones del He líquido superfluído. Por otra parte, la existencia de vórtices y el conocimiento de la física que los describe constituyen la base de la ingeniería de materiales superconductores apta para diseñar aplicaciones tecnológicas.
Ni aun los científicos más audaces imaginaron, en el momento del descubrimiento de la superconductividad en óxidos de Cu, que el estudio del estado mixto en estos materiales (SAT) daría lugar a la aparición de una nueva física.
La teoría de Abrikosov considera los vórtices como objetos magnéticos que, en equilibrio termodinámico, permiten la relajación de la presión del campo magnético exterior, excluido por las corrientes Meissner. A partir de un campo magnético "crítico inferior", Hc1(T), la menor energía libre del superconductor corresponde al estado mixto que se genera mediante la penetración de vórtices. La cantidad de vórtices, en equilibrio, está determinada por las dos variables termodinámicas que suele adoptar la teoría, el campo magnético, H, y la temperatura, T. Esto no es siempre correcto debido al carácter magnético de la superconductividad. Al analizar resultados experimentales es importante considerar los efectos de la forma de la muestra, para asegurar cuáles son las variables termodinámicas a decuadas al experimento que se estudia. De hecho, la mayoría de los estudios de los SAT en monocristales se hacen en muestras con geometrías donde la forma puede jugar un papel importante.
Las propiedades esenciales que caracterizan el estado superconductor se ponen de manifiesto al estudiar el comportamiento del estado mixto, en su forma elemental: un vórtice aislado. El vórtice tiene asociado un campo de velocidades, v(x), de trayectorias concéntricas (en el caso isotrópico son circunferencias) con una divergencia de la intensidad de la velocidad en una línea que definiremos como eje del vórtice. El campo de velocidades se extiende hasta distancias caracterizadas por la longitud que determina el rango de variación de campo y corriente, (T).
Cuando la temperatura es menor que la crítica, Tc(H), el parámetro de orden termodinámico ![]() (X) de la teoría de Ginsburg - Landau adquiere valores finitos, indicando la existencia de una densidad finita de pares de Cooper, dada por |
(X) de la teoría de Ginsburg - Landau adquiere valores finitos, indicando la existencia de una densidad finita de pares de Cooper, dada por |![]() (X)|2= ne. Como consecuencia, el campo de velocidades tendrá asociado una densidad de corriente superconductora J=|
(X)|2= ne. Como consecuencia, el campo de velocidades tendrá asociado una densidad de corriente superconductora J=|![]() (X)|2 2e v(x).
(X)|2 2e v(x).
La energía cinética de los pares de Cooper aumenta con el cuadrado de la velocidad al aproximarse al eje del vórtice. El aumento de energía cinética compite con la energía de formación de los pares. El mantenimiento de la densidad de pares correspondiente al estado libre de vórtices se hace inestable a partir de alguna distancia del eje del vórtice. Como consecuencia de esto, el parámetro de orden depende de la coordenada, disminuye con el incremento de la velocidad y se anula en el eje del vórtice. El incremento de energía cinética y la depresión de la densidad superconductora en un núcleo alrededor del centro del vórtice es el requerimiento necesario para disminuir la presión de campo magnético, correspondiente al estado Meissner. El rango de variación espacial de (X) está determinado por la longitud de coherencia (T) del estado superconductor. La forma general de un vórtice la esquematizamos en la fig. 1.
FIGURA 1
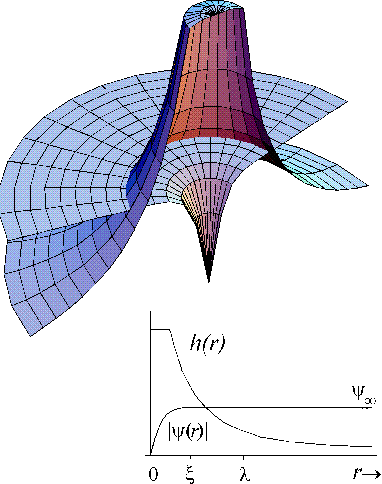
Figura 1. Esquema de la variación espacial del parámetro de orden y el campo magnético en la proximidad de un vórtice.
En la teoría de G-L se define un parámetro k=(T) / ![]() (T), que caracteriza las propiedades del material superconductor. Es evidente que cuanto mayor sea
(T), que caracteriza las propiedades del material superconductor. Es evidente que cuanto mayor sea ![]() (T) con relación a
(T) con relación a ![]() (T) más fácil resultará la creación de vórtices pues se disminuye la presión ejercida por el campo exterior sin necesidad de perder energía de condensación de pares, salvo en el volumen determinado por
(T) más fácil resultará la creación de vórtices pues se disminuye la presión ejercida por el campo exterior sin necesidad de perder energía de condensación de pares, salvo en el volumen determinado por ![]() 2(T) x L, donde L es el largo del vórtice. Los SAT se caracterizan por tener valores muy altos de k (>>100).
2(T) x L, donde L es el largo del vórtice. Los SAT se caracterizan por tener valores muy altos de k (>>100).
Cuando se aumenta el número de vórtices en el superconductor, como respuesta al incremento de H, se ponen de manifiesto interacciones repulsivas entre vórtices, de carácter electromagnético, que dan origen a configuraciones geométricas periódicas de la distribución de vórtices, con orden topológico de largo alcance. Se demostró que la red hexagonal minimiza la energía del conjunto de vórtices en un material isotrópico y su presencia ha sido verificada experimentalmente (ver fig. 2).
FIGURA 2

Imagen de la red de vórtices obtenida mediante decoración magnética de Bitter en un monocristal de 2H-NbSe2. (gentileza Flavio Pardo)
La presencia de vórtices y su distribución periódica en sistemas perfectos permite vislumbrar algunas de sus propiedades. A temperatura nula los vórtices en la red ocupan lugares de alta simetría y el orden de largo alcance topológico minimiza la energía de interacción. Tal como ocurre en una red atómica, desviaciones de las posiciones de equilibrio aumentan la energía interna y dan lugar a fuerzas de restitución que, en este caso se manifiestan en variaciones locales de las corrientes y del parámetro de orden. Si los desplazamientos de los vórtices son pequeños la respuesta de fuerzas será proporcional a los desplazamientos. Los coeficientes que relacionan desplazamiento con fuerza son las constantes elásticas de la red de vórtices, que dependen de temperatura y campo. En el caso general las constantes elásticas son tensores. Debido a la simetría de la red de vórtices, intrínsecamente anisotrópica aun para el caso de materiales isotrópicos, la constante elástica asociada al desplazamiento de la dirección de los vórtices con relación a la del campo, C44, difiere de la de cizalladura, C66. Las variaciones de densidad de vórtices están determinadas por C11.
Para poder calcular las propiedades de la red de vórtices es necesario tener ecuaciones que describan las variaciones espaciales de las corrientes eléctricas y del parámetro de orden. La adecuación de la teoría de Landau de transiciones de fase de segundo orden a la superconductividad dio origen a la teoría G-L, que provee una excelente descripción de las propiedades de los superconductores convencionales. La energía libre debe describir las propiedades termodinámicas y electrodinámicas, por lo cual el cálculo del parámetro de orden (X) y de las corrientes eléctricas debe hacerse en forma autoconsistente.
En el marco de la teoría G-L, la minimización de la energía libre con respecto a los dos parámetros que la describen, ![]() (X), y el vector potencial magnético A(x), da lugar a dos ecuaciones diferenciales acopladas, cuyas soluciones proveen los valores de los dos parámetros que describen la termodinámica de equilibrio. De esta forma se obtiene la nueva ecuación constitutiva del estado superconductor, relacionando las corrientes con el vector potencial. Con la ecuación constitutiva y mediante las ecuaciones de Maxwell se encuentra la respuesta electromagnética que, dentro de la aproximación de campo medio, describe las propiedades superconductoras del material.
(X), y el vector potencial magnético A(x), da lugar a dos ecuaciones diferenciales acopladas, cuyas soluciones proveen los valores de los dos parámetros que describen la termodinámica de equilibrio. De esta forma se obtiene la nueva ecuación constitutiva del estado superconductor, relacionando las corrientes con el vector potencial. Con la ecuación constitutiva y mediante las ecuaciones de Maxwell se encuentra la respuesta electromagnética que, dentro de la aproximación de campo medio, describe las propiedades superconductoras del material.
Para comprender mejor el alcance de la teoría de G-L vamos a especificar los parámetros termodinámicos que determinan el estado superconductor en presencia de un campo magnético exterior H, los campos críticos que determinan su diagrama de fases H-T y la ecuación constitutiva entre campo y corriente.
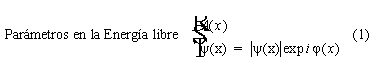
A(x) es tal que B = rot A
Nótese que el parámetro de orden es complejo. Esto no es usual en el análisis de la termodinámica de la materia condensada. Tanto el módulo como la fase pueden depender de la coordenada. La existencia de un parámetro de orden complejo es condición necesaria para describir el estado superfluído, ya que las corrientes no disipativas obedecen a ecuaciones constitutivas determinadas por las variaciones espaciales de la fase del parámetro de orden, en forma similar a la corriente de probabilidad en la mecánica cuántica. A través de esa dependencia se ponen de manifiesto las propiedades macroscópicas cuánticas que determinan el estado superfluído.
Una vez minimizada la energía, los parámetros superconductores adquieren sus valores de equilibrio que, en general, dependerán de H y T.
En la descripción de G-L hay un campo "crítico superior", Hc2(T), por encima del cual no hay superconductividad, el parámetro de orden se anula a través de una transición termodinámica de segundo orden. Las fluctuaciones termodinámicas asociadas a esta transición son sólo de carácter gaussiano, dentro de la aproximación mencionada. La misma teoría determina cuál es el campo Hc1(T) ( en el cual la energía libre del estado Meissner coincide con aquella correspondiente a permitir que ingrese un vórtice). Los campos críticos superior e inferior quedan expresados por
(2)
donde o = hc / 2e es el cuanto de flujo. Es interesante notar que Hc2(T) queda determinado por (T), mientras que, salvo por la dependencia logarítmica en k, Hc1(T) está determinado por la propiedad superconductora que determina la variación espacial de campo y corriente. Analicemos las razones para ello. En la aproximación de campo medio, la transición continua en Hc2(T) se debe a que al aumentar la intensidad del campo exterior los vórtices se aproximan a distancias entre sí menores que (T). La proporción de núcleo de vórtice frente al material donde no está deprimido el parámetro de orden cambia como H / Hc2(T), con lo cual para H![]() Hc2(T) tenemos
Hc2(T) tenemos ![]() (T)
(T)![]() 0, linealmente con H. Como las corrientes superconductoras son cuadráticas en
0, linealmente con H. Como las corrientes superconductoras son cuadráticas en ![]() (T), tienden a cero más rápido que el parámetro de orden. De ahí que el campo crítico superior no contenga información sobre el comportamiento de las corrientes. Por el contrario Hc1(T) queda determinado por la energía involucrada al introducir un vórtice cuando el campo está totalmente excluido por el estado Meissner. Es comprensible que la energía asociada a la presencia del vórtice contenga la contribución de la energía cinética y campo generado por la corriente superconductora de los pares, extendida espacialmente en una distancia del orden de
(T), tienden a cero más rápido que el parámetro de orden. De ahí que el campo crítico superior no contenga información sobre el comportamiento de las corrientes. Por el contrario Hc1(T) queda determinado por la energía involucrada al introducir un vórtice cuando el campo está totalmente excluido por el estado Meissner. Es comprensible que la energía asociada a la presencia del vórtice contenga la contribución de la energía cinética y campo generado por la corriente superconductora de los pares, extendida espacialmente en una distancia del orden de ![]() (T).
(T).
FIGURA 3
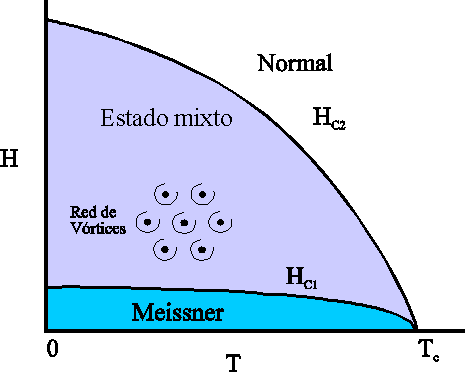
. Diagrama de fases esquemático H-T de los superconductores convencionales.
Si la aproximación de campo medio no fuese suficiente para describir las fluctuaciones termodinámicas, la física de los superconductores no estaría bien descripta por la teoría de G-L al aproximarse el campo Hc2(T). Este es un aspecto fundamental que hay que tener en cuenta en los SAT.
Cuando el campo o la temperatura son disminuidos por debajo de la línea Hc2(T), se nuclea la red deAbrikosov.
Para una mejor comprensión del efecto de la energía térmica en las redes de vórtices en los SAT, es pertinente escribir la corriente superconductora en función de las variaciones espaciales de la fase del parámetro de orden. De acuerdo a G-L
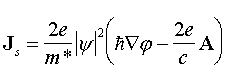 (3)
(3)
donde m* = 2m la masa de los pares de Cooper. Desde un punto de vista formal la presencia del vector potencial, A, en la expresión (3) se debe a que la corriente es una cantidad física medible, por lo cual debe ser invariante de medida. Desde un punto de vista adecuado a la descripción de resultados experimentales, la ecuación (3) es la relación constitutiva entre corriente eléctrica y campo. Dentro de la aproximación utilizada, vemos que la respuesta entre corriente y campo (en este caso el campo es el vector potencial) es lineal. Es instructivo comparar esta ecuación con la resultante de calcular la corriente de probabilidad cuántica de una partícula cargada en un campo magnético. La manifestación de las propiedades cuánticas a nivel macroscópico en la superconductividad es evidente, aun al describir una corriente eléctrica que se deduce de una minimización de la energía libre.
La ecuación (3) constituye la base de las características del comportamiento de un vórtice aislado. Debido a las propiedades del parámetro de orden, su variación espacial al recorrer cualquier trayectoria cerrada deberá ser tal que recupere su valor, salvo variaciones de la fase en múltiplos de 2;. El módulo debe ser el mismo pues así se asegura que la densidad de pares superconductores esté bien definida. La posibilidad de que cambie la fase introduce importantes consecuencias físicas. Esto se hace evidente al integrar la fase en un circuito cerrado. Utilizando la expresión (3) resulta
 (4)
(4)
donde es el flujo en el area de integración y es un número entero.
Si la fase no cambia al cerrar el circuito (estado =0) no existen singularidades. La energía libre se minimiza haciendo que el parámetro de orden sea finito en todo el material. El campo magnético es expulsado como consecuencia de la presencia de corrientes Meissner que circulan a distancias (T) de la superficie. El estado termodinámico que hemos descripto, libre de vórtices, es el estado Meissner. En este estado se pueden introducir corrientes de transporte sin generar disipación, siempre que la fase del parámetro de orden pueda cumplir con el requerimiento impuesto por (4).
Es evidente que la existencia de vórtices caracterizados por 0 generan corrientes superconductoras que crean campos magnéticos y, por ende, flujos magnéticos que deben cumplir con la condición (4). La generación de vórtices puede ocurrir bajo dos circunstancias diferentes:
-Por un lado, cuando la presencia de un vórtice produce un estado de energía equivalente a la del estado Meissner, H=Hc1(T). En este caso, y para campos mayores, la generación de vórtices disminuye la energía libre con respecto a la del estado Meissner.
-Por otra parte, se podría considerar al vórtice como una excitación del estado Meissner. El número de vórtices podría fluctuar y su valor medio producir un aumento de entropía, con la consiguiente disminución de energía libre.
De ocurrir esto resultaría que el estado Meissner es inestable frente al estado mixto, a temperaturas finitas. Sin embargo, en la aproximación de campo medio, teniendo en cuenta el incremento de energía interna que acarrea la fluctuación del número de vórtices se concluye que en una muestra masiva el estado Meissner es estable y que Hc1(T) es un campo bien definido, separando una región del diagrama de fases sin singularidades, de otra donde el equilibrio termodinámico las requiere. Es también simple entender que la forma de incrementar el número de singularidades, ![]() , minimizando la energía del campo magnético generado en el vórtice, es haciendo
, minimizando la energía del campo magnético generado en el vórtice, es haciendo ![]() =1 en cada vórtice. De esa forma la inducción magnética en el superconductor está dada por B=n
=1 en cada vórtice. De esa forma la inducción magnética en el superconductor está dada por B=n![]() 0. Donde n es el número de vórtices por unidad de área.
0. Donde n es el número de vórtices por unidad de área.
La energía asociada con un vórtice tiene, como se dijo, una contribución cinética, una magnética y otra inducida por la disminución del parámetro de orden en el núcleo. Vemos así que la menor energía interna por vórtice se consigue cuando los vórtices están paralelos al campo aplicado. Consecuentemente el estado mixto ideal de un superconductor a temperatura nula lo conforma una red de vórtices paralelos, formando la estructura hexagonal en la dirección perpendicular al campo (ver fig. 4).
De la conservación de flujo impuesta por (4) concluimos que el parámetro de red está dado por
(5)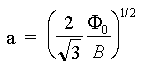
Si se ejerce una fuerza uniforme sobre una estructura de vórtices perfecta en la dirección perpendicular al campo esta se desplazará con referencia a un eje de coordenadas fijo a la estructura atómica del material. El sistema de vórtices permite su desplazamiento sobre la red atómica debido a que ésta, en el tratamiento que hemos hecho, no mantiene ninguna correlación energética con la primera.
El paso de una corriente eléctrica inducida desde el exterior (corriente de transporte) ejerce una fuerza sobre la red de vórtices. Si la red se desplaza se genera disipación a niveles muy comparables al que corresponde al estado normal. Bajo estas condiciones un superconductor es un mal conductor.
Es importante romper la simetría de traslación de la red de vórtices para poder obtener un estado que permita el paso de corriente sin disipación de energía. Para ello, se introducen defectos en la red atómica capaces de interactuar con los vórtices. En general, los defectos efectivos son aquellos que perturban la estructura electrónica del material disminuyendo o anulando la temperatura crítica en regiones espaciales con forma y tamaño parecidos al núcleo del vórtice. Bajo estas circunstancias la energía libre de la red de vórtices se minimiza tratando de poner los núcleos de los vórtices sobre los defectos (centros de anclaje). La efectividad de los centros de anclaje no depende solamente de las características del defecto, sino también de la competencia entre la energía de condensación que se gana al poner el núcleo del vórtice sobre la región con Tc disminuida y el incremento de energía elástica que necesariamente se induce al producirse el desplazamiento de los vórtices para aprovechar la energía de anclaje.
Por razones de espacio no entraremos en detalles sobre resultados experimentales y teóricos que describen las distintas posibilidades y tipos de anclaje. Sí mencionaremos que es un tema de interés en la actualidad, no solo por las posibles aplicaciones tecnológicas que se derivan de su conocimiento sino, también, porque el desplazamiento de una red periódica de vórtices sobre un potencial desordenado sirve de modelo experimental y teórico para describir variados problemas de la física moderna.
A los fines perseguidos en este artículo es necesario remarcar que una vez que la red de vórtices se encuentra distorsionada para aprovechar los centros de anclaje hará falta una fuerza finita para moverla. Cuando circula una densidad de corriente de transporte por el material se ejerce una fuerza del tipo Lorentz, de la forma
F = 1/c (JxB)
Cuando la fuerza de anclaje es igualada por FL se alcanza la densidad de corriente crítica Jc. Para J > Jc la fuerza de Lorentz sobrepasa la de anclaje, los vórtices se desplazan y originan disipación. Esta es la forma tradicional de definir la corriente crítica en un superconductor y la descripción aceptada de la disipación en los superconductores convencionales. En consecuencia, cuanto más rígida sea la red de vórtices menores serán las corrientes críticas o, a la inversa, una red blanda permitirá fijar los vórtices a los centros de anclaje que tengan más cercanos.
Estas ideas razonables, que tienen aplicación en la superconductividad convencional, tomadas como leyes inviolables, acarrearon graves inconvenientes para el progreso del entendimiento del comportamiento de las estructuras de vórtices en los SAT.
Antes de enfocar nuestro análisis a la problemática introducida por los SAT es conveniente reflexionar sobre algunas propiedades generales de la red de vórtices en la superconductividad convencional. Las constantes elásticas de la red de vórtices describen la susceptibilidad generalizada que determina la respuesta a una fuerza que induce deformaciones en la red. Como tal, sus valores dependen de cada material. Por otra parte, a diferencia de lo que ocurre en las redes atómicas, el parámetro de la red de vórtices se ajusta con el campo magnético exterior, ec. (5). Como el parámetro de red diverge en H = Hc1(T) y las fuerzas electromagnéticas tienen un rango finito, (T), las constantes elásticas tienden a cero para H![]() Hc1(T) y la red se deformará fácilmente. En el campo Hc2(T) también se ablanda la red. En este caso la distancia entre vórtices se aproxima a
Hc1(T) y la red se deformará fácilmente. En el campo Hc2(T) también se ablanda la red. En este caso la distancia entre vórtices se aproxima a ![]() (T) <<
(T) << ![]() (T). Bajo estas circunstancias no habrá modulación de campo y la posición de un vórtice es esencialmente independiente del vecino. La red de vórtices se ablanda, permitiendo que se acomoden y optimicen la fuerza de anclaje. En los superconductores convencionales se observa un aumento de la corriente crítica poco antes de alcanzar Hc2(T), donde la corriente crítica se anula debido a la anulación del parámetro de orden. La corriente crítica pasa por un máximo antes de reducirse a cero en Hc2(T).
(T). Bajo estas circunstancias no habrá modulación de campo y la posición de un vórtice es esencialmente independiente del vecino. La red de vórtices se ablanda, permitiendo que se acomoden y optimicen la fuerza de anclaje. En los superconductores convencionales se observa un aumento de la corriente crítica poco antes de alcanzar Hc2(T), donde la corriente crítica se anula debido a la anulación del parámetro de orden. La corriente crítica pasa por un máximo antes de reducirse a cero en Hc2(T).
Hagamos un resumen de las propiedades de la red de vórtices:
- Cuando la red es ideal tenemos una estructura ordenada, con orden topológico de largo alcance. La red, inestable a la acción de fuerzas, cuando se desplaza disipa. En estas circunstancias la corriente no queda determinada por la diferencia de fases del parámetro de orden y decimos que la disipación se produce por haber perdido la coherencia de la fase.
- Cuando se introducen defectos se destruye el orden topológico de largo alcance. Por otra parte, la red responde elásticamente a la presencia de fuerzas, permitiendo el paso de corrientes no disipativas. Es importante darse cuenta que la pérdida del orden topológico de la estructura permite que se establezca orden de largo alcance en la fase del parámetro de orden. El superconductor mantiene la coherencia de fase. Estrictamente el argumento anterior es válido solamente a T=0 pero para los fines prácticos puede aceptarse el argumento como buena aproximación en todo el rango de temperaturas, hasta Tc.
No hay comentarios:
Publicar un comentario