domingo, 21 de marzo de 2010
Jhon Ender Duque V CRF
Su estructura cristalina natural, comparada con la de la mayoría de superconductores clásicos, que son
generalmente metales elementales o aleaciones metálicas, es compleja. Esta formada por un apilamiento de
capas de átomos de distinta naturaleza. Para comprender mejor el papel de estas capas, los investigadores
empezaron a manipular dichos óxidos y a fabricar unas estructuras artificiales, las superredes
superconductoras. Estas superredes están formadas por capas delgadas del superconductor a estudiar,
alternando con capas de otros materiales, cuya composición y cuyo espesor se hacen variar a voluntad.
Para comprender mejor los nuevos materiales que han ido apareciendo en los últimos años hay que dilucidar
la relación entre su estructura cristalina y su superconductividad. Ahí es donde ha resultado muy útil la
fabricación "a medida " de apilamientos de finas capas de tales superconductores : las superredes. ¿que son
las superredes?. Partiendo de la idea de que los óxidos superconductores de alta temperatura cristalina por si
mismos en l estructura en capas, era tentador para el experimentador invertir en la formación de dichas capas,
modificar su apilamiento natural y su composición química, a fin de construir toda una panoplia de materiales,
las superredes, auténticos híbridos que ayudarían a forjar los conceptos importantes.
Estas estructuras artificiales están formadas por superposición de capas ultradelgadas de uno o mas
compuestos, superconductores o no. Cada capa consta de un numero variable de planos atómicos, que puede
estar comprendido entre uno y varias decenas. Cuando una capa es lo bastante gruesa, los planos atómicos se
disponen por si mismos como en el material masivo, y se esta en presencia de una doble periodicidad en la
dirección perpendicular a las capas. La periodicidad creada artificialmente, de Ahí el nombre de superred.
Las superredes de óxidos superconductores fueron realizadas por primera vez en la Universidad de Ginebra en
1989 y luego muy rápidamente al año siguiente en Estados Unidos.
La temperatura critica disminuye rápidamente al aumentar la distancia entre capas superconductoras
sucesivas. Esta explosión de actividades esta ligada a las sorprendentes posibilidades que ofrecen las técnicas
de punta de posición de capas delgadas, con la epitaxis por pulverización catódica o por chorros moleculares.
Esta ultima técnica debe sus rápidos progresos a las exigencias de la fabricación de las superredes
semiconductoras.
¿ De que se trata? Es un recinto a vacío, se dirigen uno o varios chorros de átomos o de moléculas sobre un
substrato en el que se depositan. A medida que los átomos van llegando, se va construyendo el cristal, que
7
puede formarse sin ningún defecto si el proceso se lleva cabo cuidadosamente. Para formar las superredes de
óxidos superconductores, los chorros contienen una mezcla de los átomos necesarios en proporciones
calculadas de antemano. El amontonamiento de losa tomos puede detenerse en todo momento tras el deposito
de un cierto numero de planos atómicos, para proceder luego al deposito de otra capa de distinta composición.
Aplicando tales técnicas a los óxidos superconductores, cabe pensar en fabricar estructuras dentro de las
cuales se ha modificado el numero de planos CuO2 de una malla elemental (en los materiales masivos, la
temperatura critica depende del numero de planos de CuO2 por malla elemental). También se puede cambiar
la secuencia de apilamiento entre los grupos de planos de CuO2 y luego observar como estos cambios
estructurales modifican la temperatura critica.
Los primeros resultados de los experimentos, en la Universidad de Ginebra 1989, superaron las previsiones
mas optimistas. El examen por rayos X demostró que las superredes preparadas por pulverización catodia
tienen una calidad cristalina superior a la de las capas simples. Se llega incluso a depositar las capas malla
elemental por malla elemental, lo cual corresponde a espesores extremadamente débiles, del orden de 12
angströms, el compuesto mas utilizado en estos experimentos ha sido, YBaCuO.
Por medio de estas superredes, en las que alternan capas de YBaCuO y de PrBaCuO se ha estudiado la
evolución de las propiedades superconductoras con el espesor de las capas. En 1990 se demuestra que la
temperatura critica decrece rápidamente cuando aumenta la distancia entre los grupos de planos de CuO2.
La superconductividad aparece pues a una temperatura mucho mas baja en una capa formada por una malla
aislada de YBaCuO que en una capa gruesa cuya temperatura es de 90ºK. para obtener una elevada
temperatura critica parece importante apilar las mallas lo cual sugiere que las mallas no se comportan
independientemente unas de otras.
Se produce un nuevo fenómeno que es un "ensanchamiento" de la transición, el material no pasa bruscamente
el estado superconductor a una temperatura dada sino que va perdiendo paulatinamente su resistencia al
disminuir la temperatura.
La interpretación de estos resultados es objeto todavía de muchas investigaciones. En cambio de la
temperatura de transición superconductora al separarse los planos de CuO2 indica que el acoplamiento entre
planos contribuye a aumentar esta temperatura. No obstante, todavía no se ha descubierto la manera de como
el acoplamiento modifica la temperatura critica. El ensanchamiento de las transición esta vinculado a la
aparición espontanea de "vórtices" de corriente en los superconductores de dos dimensiones.
Pero ¿que es un vórtice? Se trata de un torbellino de corrientes eléctricas espontaneas, las supercorrientes, que
pueden aparecer en el superconductor en ausencia de tensión aplicada. En los superconductores
convencionales, los vórtices solo aparecen en presencia de campo magnético y pueden visualizarse como
largos torbellinos de corriente que atraviesen el material.
En los óxidos superconductores, sin embargo, la situación es distinta. Ante todo, en las capas
cuasidimensionales como las que aquí nos interesan, los vórtices pueden aparecer espontáneamente en
ausencia de campo magnético.
Los vórtices nacen por pares y cada vórtice esta ligado a un antivortice en el que la corriente circula en sentido
contrario. Como la energía de un vórtice es proporcional a su longitud, cuanto mas delgadas son las capas,
mas fácil es crear estos pares vórtice/antivortice. A baja temperatura, ambos están ligados. Al aumentar la
temperatura es de esperar que estos pares se disocien a una cierta temperatura característica. El punto crucial
es que estos vórtices se volverán independientes, unos de otros, por encima de esta temperatura. Dicho
movimiento consume energía y todo ocurre como si en el material apreciase una resistencia eléctrica. La
temperatura a la que se disocian los vórtices es pues la temperatura de transición del sistema ya que, por
encima de ella, la resistencia deja de ser nula. Lo esencial es que esa temperatura de transición es mas baja
8
que la temperatura critica del material grueso. Cuanto mas delgada es la capa, mas se reduce la temperatura
critica. Así, el intervalo de temperatura en el que se encuentran los vórtices libres aumenta: es el
"ensanchamiento" observado por los investigadores. Esta transición, llamada BKT, encierra todavía muchos
misterios. Las superredes claro esta, son los instrumentos idóneos para resolver la controversia, ya que
permiten relacionar de un modo continuo la malla única y el superconductor masivo.
Jhon Ender Duque V CRF
2
La historia de la superconductividad empieza en 1911 en Leiden, Países Bajos. Allí H. Kamerlingh Onnes
desarrollo las primeras técnicas criogenicas para enfriar muestras hasta algunos grados por encima del cero
absoluto (correspondientes a cero Kelvin, es decir, menos doscientos, setenta y tres grados centígrados). Fue
el primero que consiguió llevar el helio hasta debajo de su punto de luciefaccion (4,2ºK), abriendo así el
campo de las bajas temperaturas. Al principio, Kamerlingh Onnes "monopolizó" completamente este campo,
ya que Leiden fue, hasta 1923, el único lugar del mundo que disponía de helio liquido.
En aquellas épocas se sabia que los metales tiene una resistividad que disminuye de manera prácticamente
lineal con la temperatura hasta unos veinte Kelvin, y se quería saber que ocurría con esta resistividad en las
proximidades del cero absoluto: ¿seguía decreciendo linealmente? ¿tendía, quizás, a un valor constante? O
bien ¿ se remontaría hacia valores muy elevados, característicos de un comportamiento aislante en vez de
conductor? Kamerlingh Onnes se dio cuenta muy pronto de que era necesario disponer de metales muy puros,
si quería obtener resultados libres de toda ambigüedad. Eligió el mercurio, elemento que puede conseguirse
con un alto grado de pureza mediante sucesivas destilaciones y que además es conductor en estado metálico.
De este modo, y enfriando el mercurio a muy baja temperatura, pudo observar un fenómeno nuevo y
totalmente inesperado: a una temperatura de 4,2ºK, el mercurio pasaba bruscamente a un estado en el que,
repentinamente, no ofrecía resistividad alguna al paso de la corriente eléctrica. Esta transición se manifestaba
por una caída muy brusca de la resistividad. Kamerlingh Onnes había descubierto la superconductividad.
Poco después se observo que la misma transición al estado de superconductor se producía en otros metales,
como el plomo o el niobio, a temperaturas criticas ligeramente mas altas. Posteriormente a partir de los años
1930, la superconductividad se observo también en cuerpos compuestos, principalmente en aleaciones
intermetalicas. La elevación de las temperaturas criticas (Tc) fue prosiguiendo a lo largo de los años, con un
progreso lento pero bastante regular. En 1973 la temperatura critica mas elevada fue de 23,3 Kelvin, con una
aleación de niobio y germanio (Nb Ge). Trece años mas tarde la situación era la misma y la mayoría de los
físicos habían acabado por convencerse de que no podía llegarse mucho mas lejos.
En el año 1960 se demostró que el titanato de estroncio (SrTiO) se hace superconductor, pero con una
temperatura de transición muy baja: 0,3 Kelvin. Posteriores estudios analizados en Rüshlikon permitieron
aumentar esta temperatura critica hasta 0,8 Kelvin mediante el dopado del compuesto con niobio.
Diez años mas tardes en 1973, D.C. Johnston y sus colegas obtuvieron un resultado mas significativo con un
oxido de titanio y litio (Li−Ti−O) : una temperatura critica de 13,7 Kelvin. En 1975, A.W. Sleight y sus
colaboradores observaron una transición a 13 Kelvin en un compuesto de valencia mixta: un oxido de bario y
plomo dopado con bismuto (BaPbBiO). En esta formula el subíndice x indica la proporción de bismuto
sustituida en el plomo.
Desde 1986, fecha de su descubrimiento los superconductores de la temperatura relativamente elevadas
plantean difíciles problemas a los teóricos. Todavía no se sabe si el mecanismo responsable del agrupamiento
de los electrones por pares que esta en el origen de la superconductividad es o no similar al de los
superconductores convencionales.
APLICACIONES Y BENEFICIOS
La principal dificultad por vencer, antes de pasar a la fase de las aplicaciones, es producir hilos o bandas
relativamente flexibles de estos materiales frágiles sin alterar sus propiedades superconductoras.
El empleo de hilos superconductores podría evitar entonces el 15% de perdida de energía, por ejemplo, debida
a la resistencia de los hilos eléctricos corrientes. Podrían ser utilizadas pues grandes bobinas superconductras
(imanes) como fuente de energía, con el fin de reducir el derroche causado por los generadores actuales. Estas
bobinas pueden almacenar importantes cantidades de energía en su campo magnético. La corriente puede
circular en ellas sin perdidas, indefinidamente, siendo posible extraerla por simple apertura de un bucle de
3
corrientes.
Existen también interesantes perspectivas de aplicaciones en el campo de los circuitos integrados, donde la
velocidad de ejecución esta limitada no por los diferentes elementos del circuito, sino mas bien por las
conexiones, muy resistivas. El empleo de materiales superconductores permitirá paliar este inconveniente y
construir microordenadores mas rápidos, naturalmente a condición de que el circuito pudiera funcionar a la
temperatura del nitrógeno liquido.
El campo de los transportes por sustentación magnética también se ve afectado por las aplicaciones de los
superconductores de alto campo critico. En Japón ya han sido construidos trenes en los que la sustentación se
realiza por medio de imanes suprconductores, aunque no hay contacto entre el vehículo y el rail cuando el tren
esta en marcha. La ausencia de fuerzas de rozamiento permite obtener velocidades del orden de 400Km/h.
Cabe prever que, con el escaso coste del enfriamiento del nitrógeno liquido comparado con el helio liquido, el
interés de estos medios de transportes se vera rápidamente incrementado.
La imagnineria médica, la física de las partículas, la fusión termonuclear, ya usuarias de imanes
superconductores, serán otros campos de aplicación de los nuevos superconductores.
LA TEORÍA BCS DE LA SUPERCONDUCTIVIDAD
La teoría microscópica estándar de la superconductividad es la teoría BCS, llamada así en honor a K. Bardeen,
L. Cooper y J.R. Schrieffer, que la propusieron en 1957 ( y por la cual les fue concedido el premio Nobel en
1972). Explica perfectamente las propiedades de los materiales superconductores habituales de baja
temperatura critica (superconductores por debajo de 23ºK). El concepto básico de la teoría BCS es la idea del
emparejamiento: a una temperatura lo suficientemente baja, los electrones del metal se asocian en pares,
llamados pares de Cooper, análogos a moléculas. Para romper un par hay que suministrar una energía por lo
menos igual a su energía de enlace. No es de extrañar, pues que el superconductor no pueda absorber energías
inferiores a un cierto valor critico (llamado banda prohibida del superconductor).
Cuando una corriente eléctrica pasa a través de un metal ordinario, los electrones en movimiento pueden sr
desviados por impurezas o por los movimientos de la red cristalina. Estas colisiones son responsables de la
resistencia eléctrica del metal. pero cuando se hace pasar a un supercondcutor por una corriente eléctrica, los
pares de Cooper se mueven de un modo coherente. Simplificado, todos ellos, efectúan el mismo movimiento
(esta propiedad esta ligada al hecho de que, contrariamente a las moléculas ordinarias, los pares de Cooper se
interpenetran ampliamente).
Un electrón no puede ser desviado individualmente y la resistencia eléctrica desaparecer. Como en las
moléculas ordinarias, los pares se forman porque hay una fuerza de atracción entre los electrones. En los
superconductores de baja temperatura critica, esta atracción se debe a la interacción de los electrones con las
vibraciones de la red cristalina.
Los cuantos de estas vibraciones se llaman fonones; son los análogos de los fotones luminosos. Pero este
mecanismo particular de la atracción entre dos electrones no es un ingrediente esencial de la teoría BCS. Se
puede considerar también una interacción en que intervengan las fluctuaciones de los momentos magnéticos
de los iones de cobre. Actualmente, hay solidas pruebas en favor de la existencia de pares de Cooper en los
superconductores de alta temperatura critica. Por contra, el mecanismo de formación de estos pares es objeto
de gran controversia.
LOS SUPERCONDUCTORES DE ALTA TEMPERATURA
Desde que la superconductividad fue descubierta en 1911 y hasta 1986 no había conseguido encontrar Tc
elevadas (la mayor era de 23ºK), lo que exigía los materiales fueran enfriados a la temperatura del helio
4
liquido (4,2ºK), lo cual era muy caro y necesitaba de una tecnología muy sotisficada.
Pero en 1986 se descubre un compuesto a base de óxidos de Cobre, Lantano y Bario (ÇBaLaCuO) que se
vuelve superconductor a 35ºK. Esto provoco una fiebre de estudios en tres direcciones preferentemente. La
primera fue la búsqueda de nuevos compuestos a fin de obtener una Tc cada vez mas elevada. En 1987 se
supera la temperatura del Nitrógeno liquido (77ºK) con un compuesto a base de Itrio, Bario y Cobre que sigue
siendo el mas estudiado (YBa2Cu3O7). Fue un paso importante porque ya se comienza a pensar en sus
aplicaciones a gran escala, ya que el Nitrógeno liquido es diez veces mas barato que el Helio liquido.
La segunda dirección es la mejora de los métodos para sintetizar estos materiales.
La tercera es la comprensión de sus propiedades físicas (eléctricas, magnéticas y ópticas).
Este estudio se realiza para dos fases:
Fase normal (por encima de la temperatura critica), en la que se intenta saber si estos nuevos óxidos
metálicos pueden clasificarse como metales tradicionales.
Y Fase superconductora (por debajo de Tc), en la que se intenta determinar si las propiedades de estos
nuevos compuestos pueden ser o no descritos por la teoría clásica BCS.
La síntesis de estos materiales y su estudio sigue siendo un campo importante de investigaciones.
Las observaciones de planos atómicos sucesivos en microscopia electrónica han relevado a menudo, la
existencia de nuevas fases y se especula con la posibilidad de sintetizarlos. También se correlaciona cada vez
mejor los defectos en sentido amplio (diferencias estiquiometricas, impurezas) con el desorden y las
propiedades de los distintos compuestos.
Las estructuras cristalograficas de estas familias de óxidos de Cobre han resultado ser bastante próximas y se
caracterizan por la presencia de planos Cobre−Oxígeno llamados planos CuO2.
Debemos hacer constar que También se han sintetizado óxidos de estructuras cubicas sin Cobre o compuestos
a base de carbono, cuya estructura tridimensional y composición química no se asemejan a las de los óxidos a
base de cobre, es decir, hay varias clases de superconductores de alta temperatura critica.
Los nuevos compuestos mas prometedores vienen en forma de películas delgadas, debido a que en los
cristales usuales se pueden observar numerosos defectos de todo tipo y a todas las escalas susceptibles de
influir fuertemente en las propiedades físicas y en cambio en las capas delgadas se pueden aislar un defecto
especifico, estudiarlo e incluso sacarle provecho.
Es También en las capas débiles donde hoy se registran las mayores densidades de corriente (intensidad por
cm2 de sección).
Pero las fuertes densidades de corriente son un requisito indispensable para las aplicaciones que necesitan
corrientes importantes o campos magnéticos intensos.
Hay un limite absoluto para la densidad de corriente que puede recorrer un superconductor sin disipación de
energía. Según la teoría BCS, esta limitación viene dada por la energía cinética que adquieren los pares de
Cooper, cuando esta energía supera la de desacoplamiento, destruye los pares y con ellos la
superconductividad y restaura el efecto Joule.
TAMBIÉN hay otras causas, como impurezas o defectos cristalinos, que hacen que la densidad de corriente
5
critica medida sea inferior al limite teórico, estimado en 1010 A/cm2.
Pero es muy frecuente que la corriente critica medida disminuya en presencia de un campo magnético, por
razones que tienen que ver con la naturaleza de los defectos, que limitan su valor y con la aparición en un
campo magnético de nuevas fuentes de disipación todavía mal conocidas.
Las prestaciones son apreciadas entre los superconductores de alta y baja temperatura. Sin embargo, subsiste
el problema de desarrollar nuevos compuestos en forma de hilos reutilizables.
Los físicos tratan de comprender mejor las propiedades de estos compuestos, que son muchos mas complejas
que las de los elementos superconductores a baja temperatura.
Para el estudio en la fase normal, se concibió el nivel de Fermi, este nivel aparece por el principio de
exclusión de Pauli, que prohibe que dos electrones se encuentren en el mismo estado; ello obliga a ocupar
niveles de energía cada vez mayor, hasta uno de energía máxima, denominado nivel de Fermi. La detección
del nivel de Fermi en fase normal de los óxidos superconductores se realiza mediante el efecto fotoeléctrico o
fotoemision, es decir, la emisión de electrones arrancados al metal cuando este es irradiado por una onda
electromagnética de alta energía. La medida de la energía electrónico de que ocupan inicialmente en el
compuesto.
Pero este método no es muy fiable o muy complicado, porque es un método muy sensible a cualquier
deterioro fisicoquímico de la superficie del material.
Los resultados actuales, en el estado normal, ascienden en establecer la existencia de una energía máxima para
los fotoelectrones lo cual es compatible con la existencia con un nivel de Fermi. Los experimentos ópticos en
el infrarrojo ayudan. Si el metal es conductor perfecto, toda la luz se refleja a causa de la completa libertad de
movimiento de los electrones, coas que no ocurre en un metal ordinario. Es decir, hay una relación directa
entre la conductividad de un metal y su capacidad de reflejar la luz.
Para comprender la fase normal, se siguen dos caminos:
El primero es mejorar la descripción en términos de líquidos de Fermi o habrá que renunciar totalmente a ella.
Este ultimo punto de vista es el que ha adoptado hace ya varios años el teórico P.W. Anderson, de la
Universidad de Princeton, en Estados Unidos. SEGÚN él, contrariamente al caso del liquido de Fermi, en el
que los electrones son portadores de una carga eléctrica y de un "espin" (momento cinético intrínseco), estas
dos magnitudes están disociadas en el estado normal de los nuevos compuestos. El trasporte de carga correría
a cargo de los "holones" (partículas sin carga pero con espin) transportarían el espin. Por ahora este modelo
tiene una sola dimensión espacial. Se supone que estos conceptos son extensibles a la geometría
bidimensional de los planos Cobre−Oxígeno de los óxidos superconductores.
La caracterización de la fase superconductora ha progresado en gran parte gracias a la mejora de la calidad de
las muestras. En lo tocante, a estudios fundamentales, el mejor terreno, pese a su reducido tamaño, es el de los
monocristales, pues se puede acceder a todas las orientaciones cristalograficas y estudiar como las
propiedades del compuesto dependen de la dirección espacial considerada. Uno de los progresos mas recientes
ha consistido en hacer crecer monocristales carentes de ciertos defectos inherentes a la estructura metálica de
dichos materiales.
Los resultados mas notables de reflectividad en fase superconductora se obtuvieron en 1990 con un cristal
desprovisto de defectos. El equipo IBM observo en el infrarrojo lejano un coeficiente de reflexión
estrictamente igual a la unidad característico de un conductor perfecto, pero únicamente en la dirección X.
6
A partir de una cierta frecuencia, la reflecitividad deja de ser total. Es importante poder localizar dicha
frecuencia, pues de ella se deduce el valor de la banda prohibida, que corresponde a la energía necesaria para
romper un par de Cooper. Pero una predicción fundamental de la teoría BCS es que la banda prohibida
expresada en Kelvin, es igual a 3,5 veces la temperatura critica. El valor 3,5 es importante porque esta ligado
a la intensidad de reacción de los electrones, una interacción que esta en el origen de los pares de Cooper, 3,5
significa un acoplamiento débil entre la red cristalina y los pares de electrones.
La medida del equipo IBM sitúa la banda prohibida cerca de 700ºK, valor muy superior a la temperatura
critica de 90ºK. El factor de 3,5 queda pues ampliamente rebasado. Las medidas por efecto fotoeléctrico por
debajo de Tc confirma la presencia de un umbral de energía, aquí También dos veces mayor que el valor
previsto por la teoría BCS.
Actualmente se dispone de muchos experimentos que concuerdan en asignar al cociente entre la banda
prohibida y la temperatura critica un valor muy superior al que prevé la teoría BCS para un acoplamiento
débil. Estos resultados sugieren que la teoría clásica a de tener en cuenta un acoplamiento fuerte, tal vez con
los fonones, es decir, con las vibraciones de la red cristalina. Pero se consideran También otras interacciones,
por ejemplo con las fluctuaciones colectivas de los momentos magnéticos de los iones de Cobre.
Jhon Ender Duque V CRF
La superconductividad es un fenómeno que denota el estado en el cual la resistencia eléctrica de ciertos
materiales de forma repentina hasta llegar a cero. La temperatura por debajo de la cual la resistencia eléctrica
de un material se aproxima a cero absoluto se denomina temperatura critica (Tc). Por encima de esta
temperatura, al material se le conoce como normal, y por debajo de Tc, se dice que es superconductor.
Además de la temperatura el estado superconductor También depende de otras variables, como son el campo
magnético (B) y la densidad de corriente (J). De este modo, para que en material sea superconductor, la
temperatura critica del material, su campo magnético y su densidad de corriente no deben ser superadas de
unos valores específicos para cada caso, ya que para cada material, superconductor existe una superficie
critica en el espacio de T.B. y J.
Para ilustrar lo dicho anteriormente presentamos la siguiente gráfica, donde se representa la resistividad de un
material normal respecto a la temperatura, el cobre, frente a un material superconductor, como el mercurio.
Podemos observar como la resistividad del material superconductor cae bruscamente hasta un valor casi
inapreciable, mientras que la resistividad eléctrica del cobre decrece uniformemente mientras disminuye la
temperatura, y alcanza un valor mínimo a 0ºK.
Como anunciamos anteriormente la superconductividad depende del campo magnético puesto que si un
campo magnético suficientemente fuerte se aplica a un superconductor a cualquier temperatura que este por
debajo de su temperatura critica (Tc), el superconductor retorna a su estado normal. El campo magnético
aplicado necesario para restablecer la conductividad eléctrica normal en el superconductor se denomina
campo critico (Hc). La curva de Hc frente a la temperatura, T (ºK), puede aproximarse mediante la expresión:
Hc = Ho [1−(T/Tc)^2]
donde Ho es el campo critico a una temperatura T=0ºK. Esta curva representa el limite o la frontera entre los
estados normal y de superconductividad de un superconductor.
Los superconductores metálicos e intermetálicos se clasifican, según su comportamiento frente al campo
magnético aplicado, como superconductores de tipo I y de tipo II. Los superconductores del primer tipo
También conocidos como superconductores blandos, presentan un valor de Tc y de Hc demasiado bajos para
1
cualquier aplicación practica. Algunos elementos metálicos como el plomo, estaño, mercurio y el aluminio
pertenecen a este grupo. Estos son conductores perfectos a la electricidad por debajo de Tc, pero cada uno
pierde su propiedad a un valor critico del campo magnético por debajo de 1500 Oe.
Si un cilindro largo d en superconductor de tipo I como Pb o Sn se coloca en un campo magnético a
temperatura ambiente, el campo magnético penetra normalmente a través del metal. Sin embargo, si la
temperatura del conductor del tipo I se reduce por debajo de su Tc (7,19ºK para el Pb) y si el campo
magnético esta por debajo de Hc, el campo magnético es expulsado de la muestra con excepción de una capa
de penetracion muy fina de unos 10^−5 cm en la superficie. Esta propiedad de expulsión de un campo
magnético en el estado de superconducción recibe el nombre de Efecto Meissner.
Los superconductores de tipo II se comporta de forma diferente en un campo magnético a temperaturas por
debajo de la temperatura critica. Ellos son diamagneticos, como lo superconductores de tipo I, hasta un valor
de un campo magnético aplicado llamado campo critico inferior Hc1, y de este modo el flujo magnético es
rechazado del material. por encima de Hc1 el campo empieza a penetrar en el superconductor de tipo II y
continua así hasta que alcanza el campo critico superior Hc2. En el intervalo entre Hc1 y Hc2 el
superconductor esta en estado mixto y por encima de Hc2 vuelve a su estado normal.
En la región Hc1 y Hc2 el superconductor puede conducir corriente eléctrica dentro del grueso del material y
de esta forma esta región del campo magnético puede ser usada para superconductores de alto campo y alta
corriente con el NiTi y Ni3Sb que son superconductores del tipo II.
En la figura anterior se muestra el efecto Meissner antes explicado:
Cuando la temperatura de un conductor del tipo I se reduce por debajo de Tc y el campo magnético esta por
debajo de Hc, el campo magnético es completamente expedido desde una muestra, excepto en una pequeña
capa superficial.
Los superconductores del tipo I son poco transportadores de la corriente eléctrica, ya que la corriente solo
puede fluir por la capa superficial externa de una muestra conductora. La razón por la cual sucede esto es que
el campo magnético solo puede penetrar la capa superficial, y la corriente solo puede fluir por esta capa. En
los superconductores de tipo II, por debajo de Hc1, los campos magnéticos se comportan de igual manera.
Sin embargo, si el campo se encuentra entre Hc1 y Hc2 (estado mixto), la corriente puede ser transportada por
el interior del conductor en filamentos. En los superconductores de tipo II, cuando se aplica un campo
magnético entre Hc1 y Hc2, el campo atraviesa el volumen del superconductor en forma de haces de flujos
cuantizados e individuales, llamados fluxoides. Una supercorriente cilíndrica en torbellino rodea cada
fluxoide. Con el aumento de la fuerza del campo magnético, mas y mas fluxoides entran en el superconductor
y constituyen una formación periódica. Para Hc2 la estructura a base de vértices de supercorriente colapsa y el
material vuelve a su estado de la conducción normal.
Todos los materiales superconductores se pueden clasificar en tres grupos principales: elementos metálicos,
aleaciones y compuestos. Los elementos metálicos pertenecen al tipo I, y no ofrecen grandes posibilidades de
aplicaciones practicas. Sin embargo las aleaciones en especial aquellas que contiene elementos de transición
como el Nb−Zr, Nb−Ti y Mo−Re, tienen una Tc alrededor de 10ºK, y un campo magnético critico
relativamente elevado. Estas aleaciones se han utilizado en la construcción de bobinas superconductoras para
imanes. Los mas prometedores son algunos compuestos intermetalicos (anteriormente anunciados) con un
campo magnético muy elevado (210000 Oe). En el cuadro siguiente se proporcionan datos de unos cuantos
materiales superconductores seleccionados, que pertenecen tanto al tipo I con al tipo II.
Jhon Ender Duque V CRF
Existen superconductores cerámicos los cuales son materiales comúnmente denominados como perovskitas. Las perovskitas son óxidos metálicos que exhiben una razón estequiométrica de 3 átomos de oxigeno por cada 2 átomos de metal; son también típicamente mezclas de muchos diferentes metales. Por ejemplo, un caso es el superconductor Y1Ba2Cu3O7, en el cual los metales presentes son el Itrio, Bario y Cobre. Las perovskitas como material cerámico, comparten muchas propiedades con otros cerámicos
POLARIZACIÓN Y PIEZOELECTRICIDAD:
METALES SEMICONDUCTORES Y CERÁMICOS
Es importante explicar que cuando uno aplica un campo magnético a un metal semiconductor o un cerámico, se genera la formación y el movimiento de dipolos contenidos en un material. Estos dipolos son átomos o grupos de átomos que tienen carga desequilibrada, no así en el caso a de la aplicación de un campo eléctrico dichos dipolos se alinean causando una polarización. La polarización ocurre cuando un lado de este átomo o molécula se hace ligeramente más positivo o negativo que el lado opuesto, es decir, se crean dipolos debidos al campo eléctrico. Existen cuatro mecanismos de polarización:
* Polarización electrónica: Consiste en la concentración de los electrones en el lado del núcleo más cercano al extremo positivo del campo. Esto produce una distorsión del arreglo electrónico, y así el átomo actúa como un dipolo temporal inducido. Este efecto, que ocurre en todos los materiales es pequeño y temporal.
* Polarización iónica: Los enlaces iónicos tienden a deformarse elásticamente cuando se colocan en un campo eléctrico debido a las fuerzas que actúan sobre los átomos a más de las de enlaces. En consecuencia la carga se redistribuye dentro del material microscópicamente. Los cationes y aniones se acercan o se alejan dependiendo de la dirección de campo causando polarización y llegando a modificar las dimensiones generales del material.
* Polarización molecular: Algunos materiales contienen dipolos naturales, de modo que cuando se les aplica un campo giran, hasta alinearse con él. No obstante, existen algunos materiales como es el caso del titanato de bario, los dipolos se mantienen alineados a pesar de haberse eliminado la influencia del campo externo.
Anteriormente, al enunciar la polarización iónica, se menciona la posibilidad de que hubiera modificación de las dimensiones del material. Este efecto se conoce como electrostricción, además de darse por cambios en la longitud de los enlaces entre iones, puede ser resultado de la actuación de los átomos como partículas en forma oval en vez de esférica o por distorsión debida a la orientación de los dipolos permanentes de un material. Sin embargo, existen materiales que muestran una propiedad adicional, tales que cuando se les impone un cambio dimensional, ocurre polarización, lo que crea un voltaje o un campo. Los materiales que presentan este comportamiento son piezoeléctricos. Cuando se encuentran entre capas del material conductor, los materiales dieléctricos que se polarizan son capaces de almacenar cargas, esta propiedad se describe mediante dos constantes: constante dieléctrica (relación de la permisividad del material con la permisividad en el vacío) y la resistencia dieléctrica (campo dieléctrico máximo que puede mantener un material entre conductores).
La presencia de polarización en un material después de que se retira el campo eléctrico se puede explicar en función de una alineación residual de dipolos permanentes. Esto sucede al tomar un cristal cuyos dipolos se encuentran orientados de forma aleatoria, de forma que no hay polarización neta; al aplicar un campo, los dipolos comienzan a alinearse con dicho campo. Para finalizar, el campo alinea todos los dipolos y se obtiene la polarización máxima o de saturación; cuando posteriormente se retira el campo, queda una polarización remanente, debida al acoplamiento de dipolos y el material ha quedado permanentemente polarizado. En el caso de los materiales metálicos férricos, que retienen una polarización neta, una vez retirado el campo se conocen como ferroeléctricos.
Para que el material dieléctrico almacene energía, se debe impedir que los portadores de carga como iones y electrones se muevan de un conductor a otro a través de él, en consecuencia, los materiales dieléctricos tienen siempre una alta resistividad eléctrica. Materiales utilizados para aislar el campo eléctrico deben poseer alta resistividad eléctrica, alta resistencia dieléctrica y un bajo factor de pérdida. Sin embargo, una constante dieléctrica alta no es necesaria e incluso puede llegar a ser indeseable. Una constante dieléctrica pequeña impide la polarización, por lo que no se almacena carga localmente en el aislante. Esto quiere decir que únicamente los materiales poco conductores e inclusive aislantes, son capaces de polarizarse con facilidad.
PIEZOELECTRICIDAD PROPIEDAD ELÉCTRICA DE LOS CERÁMICOS
Como se pudo resaltar con anterioridad, un material piezoeléctrico muestra la propiedad, tales que cuando se les impone un cambio dimensional ocurre polarización creando un voltaje o un campo eléctrico. La piezoelectricidad es la deformidad que se produce únicamente en materiales cerámicos al incidir sobre ellos una corriente alterna de alta frecuencia, produciendo una dilatación y contracción que origina vibraciones mecánicas, comportándose así el material como un emisor sonoro. En forma resumida se puede decir que los materiales piezoeléctricos transforman la energía mecánica (o energía sonora) en energía eléctrica (efecto piezoeléctrico directo), y así lo que ocurre es que al someter el material a la acción mecánica de la compresión o tracción, las cargas de la materia se separan y esto da lugar a una polarización de la carga; o puedo ocurrir lo opuesto (efecto piezoeléctrico inverso). Esta polarización es la causante de que salten las chispas.
Para ver el gráfico seleccione la opción "Descargar" del menú superior
Efecto Piezoeléctrico Directo Efecto Piezoeléctrico Inverso
(E. Mecánica à E. Eléctrica) (E. Eléctrica à E. Mecánica)
Para que la materia presente la propiedad de la piezoelectricidad debe cristalizar en sistemas que no tengan centro de simetría (que posean disimetría) y por lo tanto que tengan un eje polar. Los gases, los líquidos y los sólidos metálicos con simetría no poseen piezoelectricidad, esto quiere decir que se va a ver más acentuada la piezoelectricidad en materiales no simétricos como los cerámicos. Si se ejerce una presión en los extremos del eje polar, se produce polarización: un flujo de electrones va hacia un extremo y produce en él una carga negativa, mientras que en el extremo opuesto se induce una carga positiva.
El alto voltaje obtenido, que es necesario para que la chispa salga, es mayor si se utilizan láminas de cristal (u otro cerámico) estrechas y de gran superficie. Las láminas estrechas se cortan de manera que el eje polar cruce perpendicularmente a dichas caras.
La corriente generada es proporcional al área de la placa y a la rapidez de la variación de la presión aplicada perpendicularmente a la superficie de la placa. El mas conocido de los materiales piezoeléctricos es el cuarzo y los más eficaces son los titanatos. Como en estos materiales se establece un campo eléctrico y se induce la polarización bajo al aplicar una fuerza mecánica, o viceversa, estos materiales son muy prácticos para utilizarlos en transductores y otros aparatos de medidas (que veremos mas adelante).
APLICACIONES
PRINCIPALES APLICACIONES DE LOS POLÌMEROS
1.- Baterías:
Una de las aplicaciones más conocidas son las baterías recargables (de litio), estas son de menor peso que las convencionales que contenían plomo y ácido sulfúrico. La aplicación del polímero en estas es que se utiliza electrodos de plástico para así evitar el desgaste mecánico asociado a la disolución/deposición del electrodo que ocurre durante el proceso de carga y descarga de las baterías comunes. Adicional a esto, se haya la ventaja que los polímeros no contienen sustancias tóxicas ni contaminantes que puedan afectar al usuario.
2.- Aplicaciones biomédicas:
El cuerpo humano es otro dispositivo en el que los polímeros conductores podría desempeñar un papel importante en el futuro debido a su alta estabilidad y a su carácter inerte se especula con la posibilidad de su utilización en prótesis neurológicas y musculares.
MUSCULOS ARTIFICIALES:
Los músculos artificiales basados en los polímeros conductores electrónicos intrínsecos fueron patentados en 1992. Las sustancias gelatinosas trabajan a muy elevados potenciales (> 20 V), necesitan dos electrodos metálicos auxiliares para crear el campo eléctrico que requieren, trabajan mediante fenómenos electrocinéticas (electroforesis y electro-ósmosis), son dispositivos electro-kineto-mecánicos en los cuales la velocidad de movimiento es baja. Los nuevos músculos artificiales son en cambio basados en polímeros conductores nos ha acercado a los músculos naturales en varios aspectos fundamentales: trabajan a bajo potencial (100 mV- 2 V) los músculos naturales a 60-150 mV, que es el potencial del pulso nervioso- , el mismo material es conductor electrónico, iónico y es actor y sensor de las condiciones de trabajo. Existe una diferencia importante entre el músculo natural y los nuevos músculos artificiales (o de segunda generación), dicha diferencia data en que el pulso eléctrico transmitido se debe a la acción de la energía química en transformación a energía mecánica producto del metabolismo (energía química-mecánica), por el contrario los músculos artificiales adquieren sus movimientos en base a la corriente eléctrica que es motor del proceso (energía eléctrica-mecánica). Además, el músculo artificial trabaja tanto en contracción como en expansión, mientras que el natural solamente trabaja en contracción.
NERVIOS ARTIFICIALES
Las señales del sistema nervioso van codificadas en pulsos iónicos tales como K+, Na+ o Ca2+, o químicos -neurotransmisores- muchos de ellos también iónicos. Para llegar a captar las "órdenes" enviadas por el cerebro para mover un brazo, y poder amplificarlas y emplearlas en mover un brazo artificial o en conseguir que un paciente no pierda masa muscular después de un accidente, se necesita un transductor ión-electrón. Los óxidos metálicos son empleados como transductores en redes neuronales, pero no son biocompatibles, lo contrario con los polímeros conductores que son biocompatibles, pero desventaja el hecho que tienden a intercambiar aniones.
El intercambio de aniones se puede transformar en un intercambio de cationes mediante una ingeniería molecular sencilla en la síntesis. Al generar eléctricamente polipirrol en presencia de un polielectrólito, como sulfato de poliestireno, carboximetil celulosa o poliacrilato sódico, se genera un material compuesto poilipirrol-polielectrolito, debido a que el polielectrolito va compensando las cargas positivas del polímero durante la generación. Al reducir el polímero los aniones no se van, ya que forman parte de una madeja polimérica entrelazada. Para mantener el principio de electroneutralidad obligamos a que penetren cationes desde el exterior para asociarse con el polianión. Durante la oxidación se expulsan los cationes.
El polímero conductor se transforma así en un transductor en el que una entrada de electrones en el material va asociada con una entrada de cationes y viceversa. Al ser un gel y comportarse, al mismo tiempo, como una membrana, los cationes presentes en el polímero- y su potencial eléctrico -dependen de la concentración en el medio. Ello quiere decir que el electrodo polimérico responde ante la concentración del medio con un potencial eléctrico, por lo que disponemos de la interfase adecuada, biocompatible y sensible, capaz de recibir señales eléctricas y transformarlas en señales iónicas, por lo tanto entendibles por el sistema nervioso, o de responder ante una variación de la concentración iónica, provocada por un pulso nervioso; transformándola en una señal eléctrica.
3.- Sensores:
Los biosensores de medición del amperaje constituyen un amplio campo de trabajo por su interés científico y sus múltiples aplicaciones biomédicas y analíticas. Las posibilidades de inmovilización de los reactivos biológicos (incluyendo enzimas, células, tejidos y anticuerpos) son muy diversas, lo que hace que existan un gran número de trabajos científicos que se publican en la actualidad sobre el tema.
BIOSENSOR
Este es un ejemplo de un sensor, en este el dopado al que se someten los polímeros es bastante sensible al calor, sufriendo así una pérdida de conductividad al calentarse. Conectándolo a una resistencia, estos polímeros permiten controlar la temperatura a la que, por ejemplo, un producto farmacéutico llega a alterarse. También se pueden usar como sensores de radiación si se colocan en una atmósfera de gases que los convierte en dopantes activos cuando son expuestos a radiación.
SENSOR ANALITICO
Este es otro tipo de sensor, en el cual como otra aplicación debida al poder de cambiadores iónicos de los polímeros conductores estos pueden ser utiles, esto se da a que los polímeros son capaces de detectar y separar iones como Hg2+ e incluso Au0 de una gran variedad de disoluciones tanto acuosas como con disolventes orgánicos.
Jhon Ender Duque V CRF
TEMPERATURA Y ESTRUCTURA: PARAMETROS QUE AFECTAN LA CONDUCTIVIDAD
Como se especificó anteriormente, la conductividad de un material se ve afectado por su estructura de bandas de energía a nivel atómico. Sin embargo, la conductividad es afectada también por el cambio de la energía cinética de los átomos o moléculas debido al amplio incremento o disminución de temperatura. De igual manera se afecta la conductividad por efecto del cambio o tipo de su estructura debido a las imperfecciones a nivel cristalino de la misma.
En el caso de los metales cuando se incrementa bastante la temperatura de este, la energía térmica hace que los átomos vibren mucho más, incrementando su energía interna (energía cinética de los átomos). Ya con esto, la movilidad de los electrones al igual que el recorrido libre medio (distancia promedio entre colisiones) se reduce, no así aumenta la resistividad del metal. La resistividad en función de la temperatura podría estimarse por medio de la siguiente ecuación:
Donde se observa una relación entre la resistividad debido a la vibración térmica por efecto de la nueva temperatura y la resistividad a temperatura ambiente, la cual se ve afectada por el cambio de temperatura y el coeficiente térmico de la resistividad.
Por otro lado, al existir defectos reticulares, es decir imperfecciones de la red cristalina, los electrones se dispersan, de este modo la movilidad de ellos disminuye y con ello la conductividad.
Para ver el gráfico seleccione la opción "Descargar" del menú superior
Como se observaría en la figura anterior, en el caso de un cristal perfecto (a), el electrón no tiene mayor problema para poder pasar a través de la red de átomos. Contrario a esto, al aumentarle la temperatura a un material (b), los electrones aumentan sus vibraciones por lo que la facilidad del electrón de poder desplazarse por la red es mucho menor. Adicional a esto, si la red tuviere imperfecciones como átomos sustitucionales (c) (generalmente en metales impuros), el electrón es dispersado causando una dificultad en la movilización a través de la misma.
EFECTO DEL PROCESAMIENTO Y DEL ENDURECIMIENTO EN UN MATERIAL METÁLICO
Por lo general, un material metálico, es procesado o endurecido, antes de ser empleado o usado para alguna aplicación técnica. Estas prácticas afectan de maneras distintas a las propiedades eléctricas de un material. En el caso del endurecimiento por solución sólida al agregar tanto átomos sustitucionales como intersticiales se puede aumentar la resistencia mecánica. No así, al incrementar la cantidad de componente aleante en un material, la conductividad se ve disminuida. Se puede dar una breve explicación a partir de la siguiente figura.
Para ver el gráfico seleccione la opción "Descargar" del menú superior
Al introducir defectos puntuales de tipo sustitucional, intersticial, o vacantes generamos el endurecimiento por solución sólida. Sin embargo, estos defectos puntuales también alteran la red. Es así como los átomos (sutitucionales e intersticiales), producen una desviación en el movimiento del electrón haciendo que el material disminuya su conductividad.
Adicionalmente, un metal puede ser endurecido por envejecimiento y/o por dispersión (componentes aleados son solutos precipitados). En estos tratamientos para endurecer un metal, la conductividad es reducida aún más. Esto se debe a que la distancia entre los precipitados es mas larga que entre defectos puntuales causados por solución sólida.
Para ver el gráfico seleccione la opción "Descargar" del menú superior
De igual manera, el endurecimiento por deformación (o por trabajo en frío) tiene su efecto sobre la conductividad. Sin embargo, por medio de este tipo de endurecimiento, la conductividad y propiedades eléctricas no se ven tan afectadas. Esto se debe que en este caso, existen regiones en los cuales el recorrido medio de los electrones es grande, por lo que la conductividad es únicamente perjudicada en secciones en las cuales los granos se hayan comprimidos y tensionados.
CONDUCCIÓN EN POLÍMEROS
Los polímeros tienen una estructura de banda con una gran brecha de energía, lo cual indica que su conductividad eléctrica es bien baja. Esto se debe a que los electrones de valencia en estos tupos de materiales toman parte en enlaces covalentes. Los polímeros por ello se utilizan en aplicaciones en los cuales se requieren aislamiento eléctrico para evitar cortocircuitos y descargas. Los polímeros en pocas palabras consisten en un buen material dieléctrico. No obstante debido a la baja conductividad, en muchos casos suelen acumular electricidad estática y crean campos electroestáticos que producen daños a los materiales que aíslan debido a las pequeñas descargas contrarias que llegan a causar.
La resistividad en un polímero puede reducirse agregando compuestos iónicos. Esto se debe a que los iones pueden viajar libremente por la superficie del polímero atrayendo partículas de agua (humedad) y disipando así la estática. Otra forma de disminuir la resistividad de un polímero es por medio de la adición de partículas de grafito u otro material de mayor conductividad. Por ocasiones, aditivos de este tipo pueden ser fibras conductoras por medio de un proceso o dopado que consiste en agregar de manera intencional un pequeño número de átomos de impureza en el material. Cuando ocurre esto se aumenta la conductividad de los polímeros convirtiéndolos en semiconductores denominados extrínsecos. Lo que ocurre es que los electrones pueden así saltar libremente de un átomo a otro a lo largo de la cadena (de carbonos, propias de los polímeros), incrementando de tal manera la conductividad lo suficiente. Específicamente entonces, un semiconductor extrínseco, es un material aislante al cual se le agrega intencionalmente (mediante dopado) una pequeña cantidad de átomos de impureza. La conductividad de dicho conducto dependerá entonces de la concentración de impureza (o dopante) que tenga el material, en este caso polímero. Ejemplo de estos materiales son los polímeros de acetal y la poliftalocianina.
CONDUCTIVIDAD EN LOS CERÁMICOS: PROPIEDADES DIELÉCTRICAS
Antes de poder especificar la conductividad propia de los cerámicos es importante poder especificar la propiedad dieléctrica que tienen estos. La mayoría de los materiales cerámicos no son conductores de cargas móviles, por lo que no son conductores de electricidad. Cuando son combinados con fuerza, permite usarlos en la generación de energía y transmisión. Por ejemplo, las líneas de alta tensión son generalmente sostenidas por torres de transmisión que contienen discos de porcelana, los cuales son lo suficientemente aislante como para resistir rayos y tienen la resistencia mecánica apropiada como para sostener los cables.
No así una subcategoría del comportamiento eléctrico aislante de los cerámicos la propiedad dieléctrica. Un buen material dieléctrico es aquel que es capaz de mantener el campo magnético a través de él y sin inducir pérdida de energía. Los materiales cerámicos es usada para la pérdida progresiva de di electricidad de alta frecuencia, usada en aplicaciones como microondas y radio transmisores. A partir de esto, los materiales dieléctricos o aislantes se emplean en los condensadores para separar físicamente sus placas y para incrementar su capacidad al disminuir el campo eléctrico y por tanto, la diferencia de potencial entre las mismas.
Como información adicional, la constante dieléctrica es la propiedad que describe el comportamiento de un dieléctrico en un campo eléctrico y permite explicar, tanto el aumento de la capacidad de un condensador como el índice de refracción de un material transparente. En tanto la constante se basa en una relación con la permitividad del material y la del vacío, denominándose permitividad relativa:
En donde la permitividad del espacio es .
TEORIA DE SUPERCONDUCTIVIDAD: MATERIALES METÁLICOS Y CERÁMICOS
Al reducir paulatinamente la temperatura de un material cerca del cero absoluto, las vibraciones entre los átomos disminuyen gradualmente hasta ser un valor nulo. A partir de esta afirmación, se puede concretar la teoría de los materiales superconductores. Esta establece que cuando ciertos cristales son llevados a temperaturas que tienden al cero absoluto, la resistividad eléctrica de aquel material se vuelve nula, de esta manera la corriente puede fluir libremente por el material (sin colisiones y en zigzag). Aun cuando no es factible reducir la temperatura hasta el cero absoluto, ciertos materiales (por lo general semiconductores e incluso materiales impuros) presentan tal comportamiento a valores por encima de dicho valor. En la siguiente figura podemos observar cual sería el comportamiento de la resistencia de un material en función de la temperatura.
Para ver el gráfico seleccione la opción "Descargar" del menú superior
En el caso de la curva A, ocurriría si la resistencia eléctrica se debe completamente a la dispersión que los electrones sufrirían por las vibraciones de la red atómica. La curva B pudiera ocurrir si las dispersiones de los electrones por las impurezas que estuvieran presentes fuesen de magnitud mayor a lo común. La curva C se produciría si los electrones de la banda de conducción, disminuyeran rápidamente al disminuir la temperatura.
Sin embargo, el cambio de conducción a superconducción se lleva acabo, únicamente cuando el material alcanza una temperatura crítica Tc, a la cual los electrones tienen una misma energía pero un spin (el ímpetu angular intrínseco de una partícula) opuesto que al combinarse forman pares. De esta manera, cuando la frecuencia de las vibraciones de los átomos dentro de la red y la frecuencia de los pares de electrones logra llegar a un movimiento armónico, ocurre la conductividad. A continuación se presenta en una tabla las temperaturas críticas de algunos materiales comunes en la ingeniería.
Jhon Ender Duque V CRF
Transiciones Termodinámicas y Coherencia de Fase en Superconductores de Alta Temperatura
Anisotropía
Una de las propiedades más destacables de los superconductores basados en óxidos de cobre es que tanto sus propiedades en el estado normal como las que corresponden al estado superconductor muestran una gran anisotropía. Esa anisotropía refleja aquella que se evidencia en la estructura atómica
Los datos experimentales indican que la conductividad eléctrica es mucho mayor en la dirección de los planos de Cu-O (dirección ab) que en la dirección perpendicular a ellos (dirección c). Tenemos así una resistividad ab y una c. Una forma de definir la anisotropía del material es a través del cociente de resistividades en sus direcciones principales h = c /ab. Estos valores cambian desde el que corresponde al YBa2Cu3O7 h50, considerado como moderadamente anisotrópico, hasta los que corresponden a los materiales de mayor anisotropía, como el Bi2Sr2CaCu2O8, en el cual el cociente h20.000 pone de manifiesto la anisotropía extrema que caracteriza a estos materiales. Hemos demorado el análisis de la influencia de la anisotropía, no porque su efecto sobre las propiedades que discutimos sea de carácter secundario sino por que la anisotropía esencialmente solo modifica cuantitativamente la manifestación de esas propiedades
Para las anisotropías mayores, las propiedades físicas de los superconductores se pueden interpretar suponiendo que la superconductividad tiene un carácter cercano al bidimensional. La superconductividad se nuclea solamente en los planos de Cu-O. Las funciones de onda de los pares de Cooper en planos vecinos se superponen débilmente, permitiendo la existencia de efecto túnel (efecto Josephson) de pares entre planos. Este acoplamiento establece el carácter tridimensional del superconductor, induciendo la coherencia de fase en la dirección c.
La descripción teórica de la superconductividad en los sistemas laminares débilmente acoplados fue desarrollada por Lawrence y Doniach para describir el comportamiento de superconductores laminares convencionales, preparados artificialmente. Utilizando conceptos presentados en la teoría se puede interpretar algunas de las características cuasi-bidimensionales de los SAT. Resultados experimentales, que se discuten en este artículo muestran que aun el sistema YBa2Cu3O7 presenta características sólo esperables, de acuerdo a las concepciones teóricas aceptadas, en sistemas mucho más anisotrópicos. Creemos importante discutir resultados que se esperaría obtener en sistemas altamente anisotrópicos pues, a nuestro entender, ponen de manifiesto el comportamiento experimental, aun en sistemas que se consideran moderadamente anisotrópicos.
En una imagen laminar se considera que los planos superconductores se acoplan a través de láminas aisladoras. Dos tipos de corrientes superconductoras se pueden sostener en el sistema: las que circulan en los planos y asociadas a los correspondientes gradientes de la fase del parámetro de orden y las que, por efecto túnel, atraviesan los planos de Cu- O. En este último caso la corriente no está determinada por gradientes. El efecto Josephson explica el paso de corriente a través de junturas aisladoras, introduciendo una relación constitutiva no lineal entre la corriente y la diferencia de fase entre láminas. No puede haber corrientes determinadas por trayectorias que se localizan entre planos, pues no puede haber estados de pares con vida media infinita en la zona aisladora.
FIGURA 1
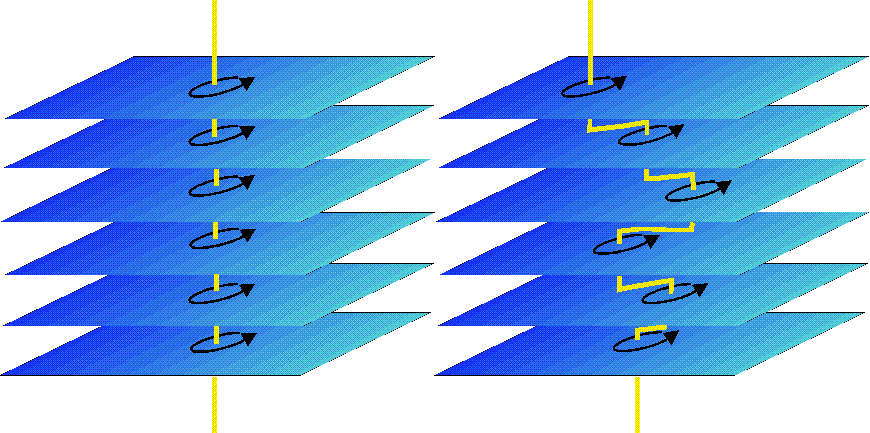
Figura 1. Esquema de la estructura de un vórtice en un SAT a temperatura nula y a temperatura finita. Las flechas representan las corrientes en los planos de CuO3
Un dibujo esquemático de cómo imaginamos un vórtice en un sistema bidimensional se muestra en la figura 2. Las corrientes se distribuyen en órbitas concéntricas sobre los planos, denominadas panqueques. Para minimizar la energía de línea del vórtice los panqueques se colocan uno encima de otro. Si las corrientes no fuesen superconductoras, esta disposición determina unívocamente la dirección del campo. Como la distancia entre planos es mucho menor que la distancia l(T) 1500 Å donde circula la corriente el resultado sería una distribución de campo indistinguible de la que corresponde a un vórtice continuo. Sin embargo, hay que tener en cuenta la relación constitutiva que gobierna la corriente superconductora. Para que no circulen corrientes en la dirección del eje c y de esa forma minimizar la energía cinética y de campo es necesario tener la fase del parámetro de orden igual entre todos los planos que constituyen la muestra laminar. Esto es, la fase cambiará en 2 en cada capa tantas veces como vórtices haya pero entre planos la diferencia de fase debe anularse.
Como los fenómenos físicos correspondientes al equilibrio termodinámico se manifiestan minimizando la energía libre y no necesariamente la interna, nos vemos obligados a analizar las excitaciones en un sistema laminar. Vimos cómo la teoría imaginaba la introducción de excitaciones de flujo magnético, en forma de toroides. Debemos pensar en formas similares que cumplan con los requerimientos de cuantificación de flujo, y que permitan introducir entropía en el sistema de panqueques. La forma más simple de introducir entropía en un sistema laminar es producir desplazamientos relativos entre panqueques en cada plano y de cada uno de ellos con relación a su vecino en el plano superior e inferior, ver fig. 2. Como al desplazarse las corrientes se introducen diferencias de fase entre planos, el desplazamiento irá acompañado de corrientes Josephson entre ellos. Como el flujo magnético debe ser conservado en forma de cuantos, las corrientes entre planos generan "vórtices Josephson" que interconectan los panqueques en los planos. Por comparación con la figura... lo que en ella eran desviaciones curvilíneas del vórtice se convierte aquí en desviaciones en forma de escalera, con dos tipos de corrientes. La energía de la excitación se compondrá de términos asociados a los panqueques y términos asociados a los tramos de vórtices Josephson.
Distinguir experimentalmente un sistema muy anisotrópico de uno laminar. es de hecho muy difícil, aunque conceptualmente son totalmente distintos. El sistema anisotrópico se describe a través de una anisotropía en los parámetros superconductores, indicando que cuesta menos energía distribuir corrientes en las direcciones ab que en c. Sin embargo un vórtice en la dirección ab tendrá corrientes superconductoras alrededor del núcleo que están contenidas en las regiones entre planos. La forma más segura de detectar un verdadero comportamiento laminar es realizar experimentos que pongan de manifiesto la existencia de junturas Josephson. Hasta ahora esto sólo se ha mostrado en los compuestos de Bi2Sr2CaCu2O8. Pese a ello, muchos resultados experimentales se pueden describir con mayor facilidad a través del modelo laminar.
Ahora que hemos discutido las características anisotrópicas de los superconductores, resulta evidente que cuanto más anisotrópico sea el superconductor más fácil será introducir excitaciones en forma de vórtices cerrados. Vemos así, la importancia que adquiere la constante C44 en la aproximación elástica del tratamiento de la interacción entre vórtices.
Propiedades de los Superconductores Convencionales
El llamado estado mixto en los superconductores tipo II ha sido objeto de intenso estudio en el pasado y en el presente. El hecho de que el estado mixto es un estado de equilibrio termodinámico fue aceptado mucho después de descubrirse el fenómeno de la superconductividad y aun después de haberse conseguido la formulación teórica que explicaba tanto su manifestación fenomenológica, a través de la teoría de Ginsburg-Landau, G-L, como su origen microscópico a través de la teoría de Bardeen, Cooper y Schrieffer, BCS.
La teoría que describe el estado mixto se debe a Abrikosov y fue dada a conocer después que Feynman describió los vórtices como excitaciones del He líquido superfluído. Por otra parte, la existencia de vórtices y el conocimiento de la física que los describe constituyen la base de la ingeniería de materiales superconductores apta para diseñar aplicaciones tecnológicas.
Ni aun los científicos más audaces imaginaron, en el momento del descubrimiento de la superconductividad en óxidos de Cu, que el estudio del estado mixto en estos materiales (SAT) daría lugar a la aparición de una nueva física.
La teoría de Abrikosov considera los vórtices como objetos magnéticos que, en equilibrio termodinámico, permiten la relajación de la presión del campo magnético exterior, excluido por las corrientes Meissner. A partir de un campo magnético "crítico inferior", Hc1(T), la menor energía libre del superconductor corresponde al estado mixto que se genera mediante la penetración de vórtices. La cantidad de vórtices, en equilibrio, está determinada por las dos variables termodinámicas que suele adoptar la teoría, el campo magnético, H, y la temperatura, T. Esto no es siempre correcto debido al carácter magnético de la superconductividad. Al analizar resultados experimentales es importante considerar los efectos de la forma de la muestra, para asegurar cuáles son las variables termodinámicas a decuadas al experimento que se estudia. De hecho, la mayoría de los estudios de los SAT en monocristales se hacen en muestras con geometrías donde la forma puede jugar un papel importante.
Las propiedades esenciales que caracterizan el estado superconductor se ponen de manifiesto al estudiar el comportamiento del estado mixto, en su forma elemental: un vórtice aislado. El vórtice tiene asociado un campo de velocidades, v(x), de trayectorias concéntricas (en el caso isotrópico son circunferencias) con una divergencia de la intensidad de la velocidad en una línea que definiremos como eje del vórtice. El campo de velocidades se extiende hasta distancias caracterizadas por la longitud que determina el rango de variación de campo y corriente, (T).
Cuando la temperatura es menor que la crítica, Tc(H), el parámetro de orden termodinámico ![]() (X) de la teoría de Ginsburg - Landau adquiere valores finitos, indicando la existencia de una densidad finita de pares de Cooper, dada por |
(X) de la teoría de Ginsburg - Landau adquiere valores finitos, indicando la existencia de una densidad finita de pares de Cooper, dada por |![]() (X)|2= ne. Como consecuencia, el campo de velocidades tendrá asociado una densidad de corriente superconductora J=|
(X)|2= ne. Como consecuencia, el campo de velocidades tendrá asociado una densidad de corriente superconductora J=|![]() (X)|2 2e v(x).
(X)|2 2e v(x).
La energía cinética de los pares de Cooper aumenta con el cuadrado de la velocidad al aproximarse al eje del vórtice. El aumento de energía cinética compite con la energía de formación de los pares. El mantenimiento de la densidad de pares correspondiente al estado libre de vórtices se hace inestable a partir de alguna distancia del eje del vórtice. Como consecuencia de esto, el parámetro de orden depende de la coordenada, disminuye con el incremento de la velocidad y se anula en el eje del vórtice. El incremento de energía cinética y la depresión de la densidad superconductora en un núcleo alrededor del centro del vórtice es el requerimiento necesario para disminuir la presión de campo magnético, correspondiente al estado Meissner. El rango de variación espacial de (X) está determinado por la longitud de coherencia (T) del estado superconductor. La forma general de un vórtice la esquematizamos en la fig. 1.
FIGURA 1
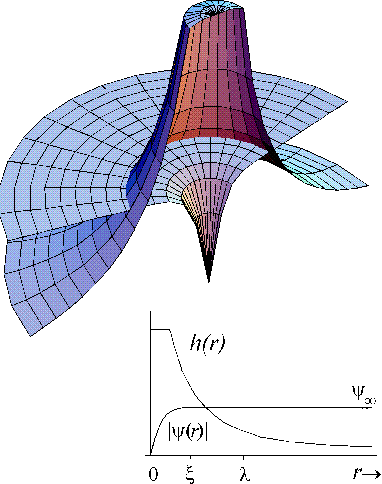
Figura 1. Esquema de la variación espacial del parámetro de orden y el campo magnético en la proximidad de un vórtice.
En la teoría de G-L se define un parámetro k=(T) / ![]() (T), que caracteriza las propiedades del material superconductor. Es evidente que cuanto mayor sea
(T), que caracteriza las propiedades del material superconductor. Es evidente que cuanto mayor sea ![]() (T) con relación a
(T) con relación a ![]() (T) más fácil resultará la creación de vórtices pues se disminuye la presión ejercida por el campo exterior sin necesidad de perder energía de condensación de pares, salvo en el volumen determinado por
(T) más fácil resultará la creación de vórtices pues se disminuye la presión ejercida por el campo exterior sin necesidad de perder energía de condensación de pares, salvo en el volumen determinado por ![]() 2(T) x L, donde L es el largo del vórtice. Los SAT se caracterizan por tener valores muy altos de k (>>100).
2(T) x L, donde L es el largo del vórtice. Los SAT se caracterizan por tener valores muy altos de k (>>100).
Cuando se aumenta el número de vórtices en el superconductor, como respuesta al incremento de H, se ponen de manifiesto interacciones repulsivas entre vórtices, de carácter electromagnético, que dan origen a configuraciones geométricas periódicas de la distribución de vórtices, con orden topológico de largo alcance. Se demostró que la red hexagonal minimiza la energía del conjunto de vórtices en un material isotrópico y su presencia ha sido verificada experimentalmente (ver fig. 2).
FIGURA 2

Imagen de la red de vórtices obtenida mediante decoración magnética de Bitter en un monocristal de 2H-NbSe2. (gentileza Flavio Pardo)
La presencia de vórtices y su distribución periódica en sistemas perfectos permite vislumbrar algunas de sus propiedades. A temperatura nula los vórtices en la red ocupan lugares de alta simetría y el orden de largo alcance topológico minimiza la energía de interacción. Tal como ocurre en una red atómica, desviaciones de las posiciones de equilibrio aumentan la energía interna y dan lugar a fuerzas de restitución que, en este caso se manifiestan en variaciones locales de las corrientes y del parámetro de orden. Si los desplazamientos de los vórtices son pequeños la respuesta de fuerzas será proporcional a los desplazamientos. Los coeficientes que relacionan desplazamiento con fuerza son las constantes elásticas de la red de vórtices, que dependen de temperatura y campo. En el caso general las constantes elásticas son tensores. Debido a la simetría de la red de vórtices, intrínsecamente anisotrópica aun para el caso de materiales isotrópicos, la constante elástica asociada al desplazamiento de la dirección de los vórtices con relación a la del campo, C44, difiere de la de cizalladura, C66. Las variaciones de densidad de vórtices están determinadas por C11.
Para poder calcular las propiedades de la red de vórtices es necesario tener ecuaciones que describan las variaciones espaciales de las corrientes eléctricas y del parámetro de orden. La adecuación de la teoría de Landau de transiciones de fase de segundo orden a la superconductividad dio origen a la teoría G-L, que provee una excelente descripción de las propiedades de los superconductores convencionales. La energía libre debe describir las propiedades termodinámicas y electrodinámicas, por lo cual el cálculo del parámetro de orden (X) y de las corrientes eléctricas debe hacerse en forma autoconsistente.
En el marco de la teoría G-L, la minimización de la energía libre con respecto a los dos parámetros que la describen, ![]() (X), y el vector potencial magnético A(x), da lugar a dos ecuaciones diferenciales acopladas, cuyas soluciones proveen los valores de los dos parámetros que describen la termodinámica de equilibrio. De esta forma se obtiene la nueva ecuación constitutiva del estado superconductor, relacionando las corrientes con el vector potencial. Con la ecuación constitutiva y mediante las ecuaciones de Maxwell se encuentra la respuesta electromagnética que, dentro de la aproximación de campo medio, describe las propiedades superconductoras del material.
(X), y el vector potencial magnético A(x), da lugar a dos ecuaciones diferenciales acopladas, cuyas soluciones proveen los valores de los dos parámetros que describen la termodinámica de equilibrio. De esta forma se obtiene la nueva ecuación constitutiva del estado superconductor, relacionando las corrientes con el vector potencial. Con la ecuación constitutiva y mediante las ecuaciones de Maxwell se encuentra la respuesta electromagnética que, dentro de la aproximación de campo medio, describe las propiedades superconductoras del material.
Para comprender mejor el alcance de la teoría de G-L vamos a especificar los parámetros termodinámicos que determinan el estado superconductor en presencia de un campo magnético exterior H, los campos críticos que determinan su diagrama de fases H-T y la ecuación constitutiva entre campo y corriente.
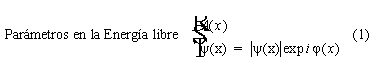
A(x) es tal que B = rot A
Nótese que el parámetro de orden es complejo. Esto no es usual en el análisis de la termodinámica de la materia condensada. Tanto el módulo como la fase pueden depender de la coordenada. La existencia de un parámetro de orden complejo es condición necesaria para describir el estado superfluído, ya que las corrientes no disipativas obedecen a ecuaciones constitutivas determinadas por las variaciones espaciales de la fase del parámetro de orden, en forma similar a la corriente de probabilidad en la mecánica cuántica. A través de esa dependencia se ponen de manifiesto las propiedades macroscópicas cuánticas que determinan el estado superfluído.
Una vez minimizada la energía, los parámetros superconductores adquieren sus valores de equilibrio que, en general, dependerán de H y T.
En la descripción de G-L hay un campo "crítico superior", Hc2(T), por encima del cual no hay superconductividad, el parámetro de orden se anula a través de una transición termodinámica de segundo orden. Las fluctuaciones termodinámicas asociadas a esta transición son sólo de carácter gaussiano, dentro de la aproximación mencionada. La misma teoría determina cuál es el campo Hc1(T) ( en el cual la energía libre del estado Meissner coincide con aquella correspondiente a permitir que ingrese un vórtice). Los campos críticos superior e inferior quedan expresados por
(2)
donde o = hc / 2e es el cuanto de flujo. Es interesante notar que Hc2(T) queda determinado por (T), mientras que, salvo por la dependencia logarítmica en k, Hc1(T) está determinado por la propiedad superconductora que determina la variación espacial de campo y corriente. Analicemos las razones para ello. En la aproximación de campo medio, la transición continua en Hc2(T) se debe a que al aumentar la intensidad del campo exterior los vórtices se aproximan a distancias entre sí menores que (T). La proporción de núcleo de vórtice frente al material donde no está deprimido el parámetro de orden cambia como H / Hc2(T), con lo cual para H![]() Hc2(T) tenemos
Hc2(T) tenemos ![]() (T)
(T)![]() 0, linealmente con H. Como las corrientes superconductoras son cuadráticas en
0, linealmente con H. Como las corrientes superconductoras son cuadráticas en ![]() (T), tienden a cero más rápido que el parámetro de orden. De ahí que el campo crítico superior no contenga información sobre el comportamiento de las corrientes. Por el contrario Hc1(T) queda determinado por la energía involucrada al introducir un vórtice cuando el campo está totalmente excluido por el estado Meissner. Es comprensible que la energía asociada a la presencia del vórtice contenga la contribución de la energía cinética y campo generado por la corriente superconductora de los pares, extendida espacialmente en una distancia del orden de
(T), tienden a cero más rápido que el parámetro de orden. De ahí que el campo crítico superior no contenga información sobre el comportamiento de las corrientes. Por el contrario Hc1(T) queda determinado por la energía involucrada al introducir un vórtice cuando el campo está totalmente excluido por el estado Meissner. Es comprensible que la energía asociada a la presencia del vórtice contenga la contribución de la energía cinética y campo generado por la corriente superconductora de los pares, extendida espacialmente en una distancia del orden de ![]() (T).
(T).
FIGURA 3
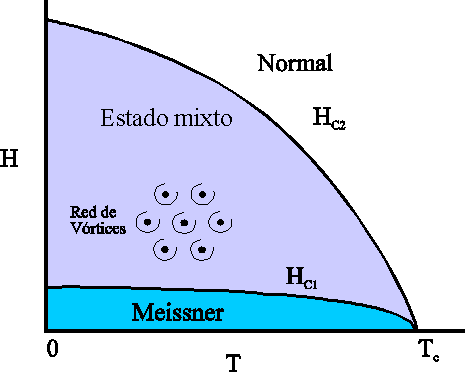
. Diagrama de fases esquemático H-T de los superconductores convencionales.
Si la aproximación de campo medio no fuese suficiente para describir las fluctuaciones termodinámicas, la física de los superconductores no estaría bien descripta por la teoría de G-L al aproximarse el campo Hc2(T). Este es un aspecto fundamental que hay que tener en cuenta en los SAT.
Cuando el campo o la temperatura son disminuidos por debajo de la línea Hc2(T), se nuclea la red deAbrikosov.
Para una mejor comprensión del efecto de la energía térmica en las redes de vórtices en los SAT, es pertinente escribir la corriente superconductora en función de las variaciones espaciales de la fase del parámetro de orden. De acuerdo a G-L
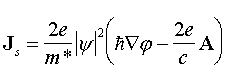 (3)
(3)
donde m* = 2m la masa de los pares de Cooper. Desde un punto de vista formal la presencia del vector potencial, A, en la expresión (3) se debe a que la corriente es una cantidad física medible, por lo cual debe ser invariante de medida. Desde un punto de vista adecuado a la descripción de resultados experimentales, la ecuación (3) es la relación constitutiva entre corriente eléctrica y campo. Dentro de la aproximación utilizada, vemos que la respuesta entre corriente y campo (en este caso el campo es el vector potencial) es lineal. Es instructivo comparar esta ecuación con la resultante de calcular la corriente de probabilidad cuántica de una partícula cargada en un campo magnético. La manifestación de las propiedades cuánticas a nivel macroscópico en la superconductividad es evidente, aun al describir una corriente eléctrica que se deduce de una minimización de la energía libre.
La ecuación (3) constituye la base de las características del comportamiento de un vórtice aislado. Debido a las propiedades del parámetro de orden, su variación espacial al recorrer cualquier trayectoria cerrada deberá ser tal que recupere su valor, salvo variaciones de la fase en múltiplos de 2;. El módulo debe ser el mismo pues así se asegura que la densidad de pares superconductores esté bien definida. La posibilidad de que cambie la fase introduce importantes consecuencias físicas. Esto se hace evidente al integrar la fase en un circuito cerrado. Utilizando la expresión (3) resulta
 (4)
(4)
donde es el flujo en el area de integración y es un número entero.
Si la fase no cambia al cerrar el circuito (estado =0) no existen singularidades. La energía libre se minimiza haciendo que el parámetro de orden sea finito en todo el material. El campo magnético es expulsado como consecuencia de la presencia de corrientes Meissner que circulan a distancias (T) de la superficie. El estado termodinámico que hemos descripto, libre de vórtices, es el estado Meissner. En este estado se pueden introducir corrientes de transporte sin generar disipación, siempre que la fase del parámetro de orden pueda cumplir con el requerimiento impuesto por (4).
Es evidente que la existencia de vórtices caracterizados por 0 generan corrientes superconductoras que crean campos magnéticos y, por ende, flujos magnéticos que deben cumplir con la condición (4). La generación de vórtices puede ocurrir bajo dos circunstancias diferentes:
-Por un lado, cuando la presencia de un vórtice produce un estado de energía equivalente a la del estado Meissner, H=Hc1(T). En este caso, y para campos mayores, la generación de vórtices disminuye la energía libre con respecto a la del estado Meissner.
-Por otra parte, se podría considerar al vórtice como una excitación del estado Meissner. El número de vórtices podría fluctuar y su valor medio producir un aumento de entropía, con la consiguiente disminución de energía libre.
De ocurrir esto resultaría que el estado Meissner es inestable frente al estado mixto, a temperaturas finitas. Sin embargo, en la aproximación de campo medio, teniendo en cuenta el incremento de energía interna que acarrea la fluctuación del número de vórtices se concluye que en una muestra masiva el estado Meissner es estable y que Hc1(T) es un campo bien definido, separando una región del diagrama de fases sin singularidades, de otra donde el equilibrio termodinámico las requiere. Es también simple entender que la forma de incrementar el número de singularidades, ![]() , minimizando la energía del campo magnético generado en el vórtice, es haciendo
, minimizando la energía del campo magnético generado en el vórtice, es haciendo ![]() =1 en cada vórtice. De esa forma la inducción magnética en el superconductor está dada por B=n
=1 en cada vórtice. De esa forma la inducción magnética en el superconductor está dada por B=n![]() 0. Donde n es el número de vórtices por unidad de área.
0. Donde n es el número de vórtices por unidad de área.
La energía asociada con un vórtice tiene, como se dijo, una contribución cinética, una magnética y otra inducida por la disminución del parámetro de orden en el núcleo. Vemos así que la menor energía interna por vórtice se consigue cuando los vórtices están paralelos al campo aplicado. Consecuentemente el estado mixto ideal de un superconductor a temperatura nula lo conforma una red de vórtices paralelos, formando la estructura hexagonal en la dirección perpendicular al campo (ver fig. 4).
De la conservación de flujo impuesta por (4) concluimos que el parámetro de red está dado por
(5)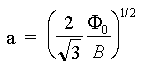
Si se ejerce una fuerza uniforme sobre una estructura de vórtices perfecta en la dirección perpendicular al campo esta se desplazará con referencia a un eje de coordenadas fijo a la estructura atómica del material. El sistema de vórtices permite su desplazamiento sobre la red atómica debido a que ésta, en el tratamiento que hemos hecho, no mantiene ninguna correlación energética con la primera.
El paso de una corriente eléctrica inducida desde el exterior (corriente de transporte) ejerce una fuerza sobre la red de vórtices. Si la red se desplaza se genera disipación a niveles muy comparables al que corresponde al estado normal. Bajo estas condiciones un superconductor es un mal conductor.
Es importante romper la simetría de traslación de la red de vórtices para poder obtener un estado que permita el paso de corriente sin disipación de energía. Para ello, se introducen defectos en la red atómica capaces de interactuar con los vórtices. En general, los defectos efectivos son aquellos que perturban la estructura electrónica del material disminuyendo o anulando la temperatura crítica en regiones espaciales con forma y tamaño parecidos al núcleo del vórtice. Bajo estas circunstancias la energía libre de la red de vórtices se minimiza tratando de poner los núcleos de los vórtices sobre los defectos (centros de anclaje). La efectividad de los centros de anclaje no depende solamente de las características del defecto, sino también de la competencia entre la energía de condensación que se gana al poner el núcleo del vórtice sobre la región con Tc disminuida y el incremento de energía elástica que necesariamente se induce al producirse el desplazamiento de los vórtices para aprovechar la energía de anclaje.
Por razones de espacio no entraremos en detalles sobre resultados experimentales y teóricos que describen las distintas posibilidades y tipos de anclaje. Sí mencionaremos que es un tema de interés en la actualidad, no solo por las posibles aplicaciones tecnológicas que se derivan de su conocimiento sino, también, porque el desplazamiento de una red periódica de vórtices sobre un potencial desordenado sirve de modelo experimental y teórico para describir variados problemas de la física moderna.
A los fines perseguidos en este artículo es necesario remarcar que una vez que la red de vórtices se encuentra distorsionada para aprovechar los centros de anclaje hará falta una fuerza finita para moverla. Cuando circula una densidad de corriente de transporte por el material se ejerce una fuerza del tipo Lorentz, de la forma
F = 1/c (JxB)
Cuando la fuerza de anclaje es igualada por FL se alcanza la densidad de corriente crítica Jc. Para J > Jc la fuerza de Lorentz sobrepasa la de anclaje, los vórtices se desplazan y originan disipación. Esta es la forma tradicional de definir la corriente crítica en un superconductor y la descripción aceptada de la disipación en los superconductores convencionales. En consecuencia, cuanto más rígida sea la red de vórtices menores serán las corrientes críticas o, a la inversa, una red blanda permitirá fijar los vórtices a los centros de anclaje que tengan más cercanos.
Estas ideas razonables, que tienen aplicación en la superconductividad convencional, tomadas como leyes inviolables, acarrearon graves inconvenientes para el progreso del entendimiento del comportamiento de las estructuras de vórtices en los SAT.
Antes de enfocar nuestro análisis a la problemática introducida por los SAT es conveniente reflexionar sobre algunas propiedades generales de la red de vórtices en la superconductividad convencional. Las constantes elásticas de la red de vórtices describen la susceptibilidad generalizada que determina la respuesta a una fuerza que induce deformaciones en la red. Como tal, sus valores dependen de cada material. Por otra parte, a diferencia de lo que ocurre en las redes atómicas, el parámetro de la red de vórtices se ajusta con el campo magnético exterior, ec. (5). Como el parámetro de red diverge en H = Hc1(T) y las fuerzas electromagnéticas tienen un rango finito, (T), las constantes elásticas tienden a cero para H![]() Hc1(T) y la red se deformará fácilmente. En el campo Hc2(T) también se ablanda la red. En este caso la distancia entre vórtices se aproxima a
Hc1(T) y la red se deformará fácilmente. En el campo Hc2(T) también se ablanda la red. En este caso la distancia entre vórtices se aproxima a ![]() (T) <<
(T) << ![]() (T). Bajo estas circunstancias no habrá modulación de campo y la posición de un vórtice es esencialmente independiente del vecino. La red de vórtices se ablanda, permitiendo que se acomoden y optimicen la fuerza de anclaje. En los superconductores convencionales se observa un aumento de la corriente crítica poco antes de alcanzar Hc2(T), donde la corriente crítica se anula debido a la anulación del parámetro de orden. La corriente crítica pasa por un máximo antes de reducirse a cero en Hc2(T).
(T). Bajo estas circunstancias no habrá modulación de campo y la posición de un vórtice es esencialmente independiente del vecino. La red de vórtices se ablanda, permitiendo que se acomoden y optimicen la fuerza de anclaje. En los superconductores convencionales se observa un aumento de la corriente crítica poco antes de alcanzar Hc2(T), donde la corriente crítica se anula debido a la anulación del parámetro de orden. La corriente crítica pasa por un máximo antes de reducirse a cero en Hc2(T).
Hagamos un resumen de las propiedades de la red de vórtices:
- Cuando la red es ideal tenemos una estructura ordenada, con orden topológico de largo alcance. La red, inestable a la acción de fuerzas, cuando se desplaza disipa. En estas circunstancias la corriente no queda determinada por la diferencia de fases del parámetro de orden y decimos que la disipación se produce por haber perdido la coherencia de la fase.
- Cuando se introducen defectos se destruye el orden topológico de largo alcance. Por otra parte, la red responde elásticamente a la presencia de fuerzas, permitiendo el paso de corrientes no disipativas. Es importante darse cuenta que la pérdida del orden topológico de la estructura permite que se establezca orden de largo alcance en la fase del parámetro de orden. El superconductor mantiene la coherencia de fase. Estrictamente el argumento anterior es válido solamente a T=0 pero para los fines prácticos puede aceptarse el argumento como buena aproximación en todo el rango de temperaturas, hasta Tc.
Jhon Ender Duque V CRF 3er Parcial
Introducción a la superconductividad eléctrica
La Superconductividad Frente al paso de una corriente electrica, los metales ofrecen una cierta resistencia: parte de la electricidad se transforma en calor y ello permite innumerables aplicaciones, como la plancha, la tostadora o elcalefactor electrico. Pero, en otros usos de la electricidad, sobre todoen su transmision a traves de cables, no resulta economico que aquella sepierda en forma de calor. En el a#o 1911 el fisico holandes Heike Kamerlingh Onnes descubrioque ciertos metales conducen la electricidad sin resistencia siempre ycuando se los haga "tiritar" cerca de la temperatura mas baja posible, unos 273 grados centigrados bajo cero. Dado que conseguir temperaturas tan bajas resulta muy costoso, elgran objetivo de la ciencia es encontrar materiales superconductores queoperen a temperaturas mas altas. Por ello, en el a#o 1986 se produjo un"boom" cuando los fisicos K. A. Muller y J. G. Bednorz encontraron queun material ceramico podia ser superconductor a una temperatura un poco masalta, unos 240 grados centigrados bajo cero. Desde entonces se han descubierto un gran numero de compuestos que presentan superconductividad si se los enfria solo con aire liquido, lo que permitira aplicaciones tecnologicas prometedoras. ¿Que se hace en superconductividad en Exactas?
Trabajando en un laboratorio de superconductividad
En el laboratorio se trabaja intensamente. Las diez o doce horas que duran las muy bajas temperaturas alcanzadas con el helio liquido deben ser aprovechadas al maximo. Ademas, previamente, se requieren unas ocho horas de preparativos. Por ello es comun que alguno de los investigadores pase la noche en el laboratorio para dejar todo listo y asi poder comenzar temprano al dia siguiente. Alli, las muestras de materiales superconductores, fabricadas porla Division de Fisica del Solido de la Comision Nacional de EnergiaAtomica, -con la que hay una estrecha colaboracion cientifica- sonsometidas a diferentes mediciones, a muy bajas temperaturas (por debajo de los 230 grados bajo cero). "Una de las tres lineas de investigacion que tenemos actualmente consiste en sacar o incorporar oxigeno en las muestras, sometiendolas a muy altas temperaturas, para ver que cambios se producen en la superconductividad", explica Bekeris. Otra de las investigaciones se basa en hacer pasar corrientes electricas desparejas a traves de una muestra, de modo que, en una parte,la corriente sea intensa, y en otra, debil. "Al medir la se#al endistintos puntos de la muestra, observamos que la corriente se organizadentro de ella", indica la investigadora, y aclara: "Lo que se mide en unlugar no depende de la corriente que pasa por alli, sino de su distribucionpor toda la muestra". Este es un experimento original del laboratorio y, segun Bekeris, puede tener aplicaciones interesantes ya que en los dispositivos que se fabriquen con estos materiales se van a producir estos fenomenos de corrientes desparejas, y es necesario saber que pasa en esas circunstancias. En el laboratorio se estudia tambien el tiempo que un material permanece magnetizado luego de ser sometido a un campo magnetico. El flujo magnetico suele quedar atrapado en los defectos del material y se va liberando de a poco. Para saber, con precision de microsegundos, cuanto tiempo le lleva liberarse, los investigadores someten a la muestra a unpulso muy corto de calor, con equipos de laser que proveen los fisicos Oscar Martinez y Mario Marconi. Este pulso de laser se aplica unos diez microsegundos despues de haber apagado el campo magnetico. Al hacer las mediciones se puede saber cuanto flujo magnetico habia, y cuanto se escapo,en ese lapso tan corto. Las peliculas delgadas de material superconductor para realizarestos experimentos son provistas por el Centro Atomico Bariloche. Para que sirve conocer cuanto tiempo queda atrapado el magnetismo? "Primero, esta es una pregunta basica, es decir que, conocer esa dinamica es conocer mas profundamente el comportamiento de estos superconductores. En cuanto a la posible relacion con aplicaciones, la famosa idea de levitacion magnetica se vincula, precisamente, con el anclaje del campo magnetico", se # a la Bekeris. La investigadora explica que, para que un material genere unafuerza repulsiva lo suficientemente intensa como para levantar su propiopeso, se necesitaria una magnetizacion muy alta, y esta puede lograrsemediante materiales que posean un gran anclaje de flujo magnetico. "Lo que estudiamos es cuanto tiempo dura el anclaje. Si este sedegrada rapidamente, no sirve", enfatiza la investigadora. Son las diez de la ma#ana, las maquinas licuefactoras se calmaron yahora comienza el verdadero trabajo, preciso y minucioso, para desentra#arlos enigmas de la superconductividad, y este es el camino obligado paraalcanzar los tan ansiados superconductores "calientes".
Fabricación por medio de reacciones en estado sólido de cerámicas superconductoras
Los materiales con características de superconductividad, presentan muy buenas expectativas respecto a su utilización en áreas donde los materiales tradicionales han encontrado sus límites. Durante 1995 se desarrolló un proyecto titulado "Conformado por Extrusión de Materiales Superconductores", donde se precisó cuantitativamente la dependencia de la estructura de la solución sólida Nd[1+x]Ba[2-x]Cu3O[7+d] y Bi2Sr[2+x]Ca[1+x]Cu2On para diferentes contenidos de oxigeno 1<=d<=0 y para algunos x selectos (0<=x<=0.5).
Las propiedades eléctricas y estructurales de estos compuestos, dependen fuertemente de la cantidad de oxígeno que contienen; muestras muy desoxigenadas, presentan más de una fase cristalina.
Luego de la obtención de los polvos con las características requeridas, se procedió a la manufacturación de elementos para comprobar sus propiedades de superconductividad.
El método de conformado fue la extrusión en matrices de acero, considerando los parámetros reológicos para la preparación adecuada de la mezcla y los de trabajo que permiten la obtención de cuerpos cerámicos manipulables, así como las condiciones de sinterización del cuerpo cerámico.
Desarrollo y fabricación de piezas a base de carburo de silicio: materiales permeables, materiales compuestos, materiales tixotrópicos.
Los avances logrados en las operaciones minero-metalúrgicas, han generado una demanda de materiales con propiedades únicas que soporten las severas condiciones de trabajo impuestas por las exigencias de mayor productividad en dichas faenas. Los materiales compuestos , cerámicos de matriz metálica, son los que satisfacen estos nuevos requerimientos de productividad y menores costos específicos de operación. El objetivo en este desarrollo fue la producción de cermets de carburo de silicio infiltrado con aleaciones de cobre. El problema esencial que se debió resolver, fue la compatibilidad de la fase cerámica con el metal o su aleación de tal forma que la infiltración ocurra ocupando debidamente los poros contenidos en la microestructura cerámica, sin que ocurra una reacción y, sin embargo, se logre una apropiada adhesión cerámica-metal. La configuración de la porosidad.